The explicit form of the Laplace equation in two-dimensional Cartesian coordinates is
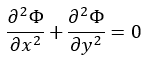 .
.
By using the separation-of-variable technique, (x, y) can be decomposed as X(x)Y(y), then the Laplace equation can be reduced to
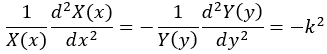
where k is a constant independent of x and y.
Possible solutions of X(x) are cos kx, sin kx, e jkx, e-jkx, and possible solutions of Y(y) are cosh ky, sinh ky, e ky, or e-ky.
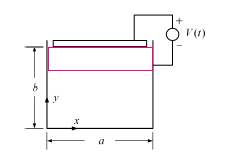
The figure shows a rectilinear trough with side and bottom walls grounded, and the top wall is connected to a voltage source, v(t). The potential distribution satisfying the boundary conditions that Φ = 0 at x = 0 and y = 0 is Φ = A sin kx sinh ky.
The boundary condition that at Φ = 0 x = a renders k = nπ/a, with n an integer. The potential can thus be expressed as
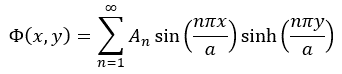 .
.
The boundary condition at y = b requires that
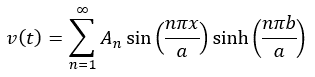 .
.
By utilizing the orthogonality property of the sin nπx/a functions, first multiply the above equation by sin mπx/a , and integrate over 0 ≤ x ≤ a to have
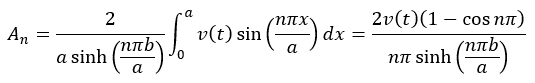 .
.
Potential Distribution
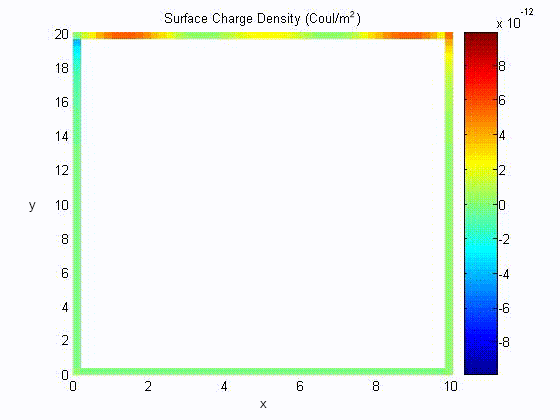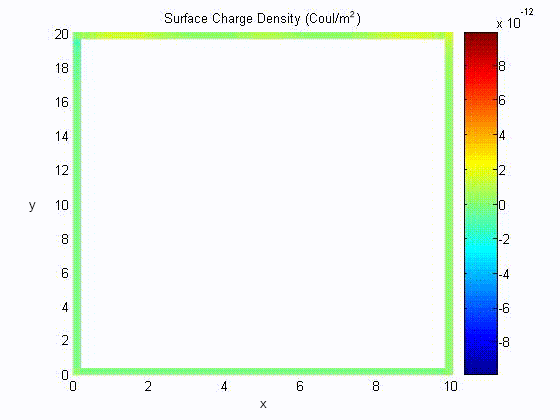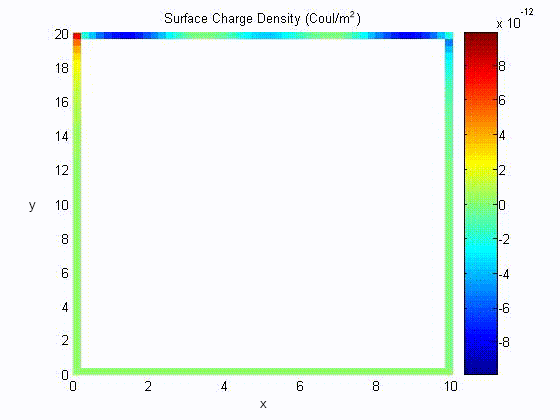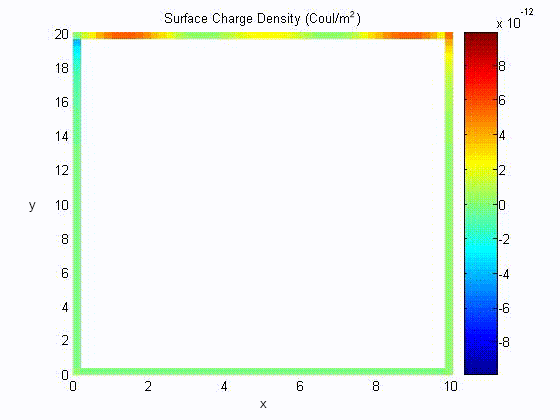
Assume a = 10, b = 20,
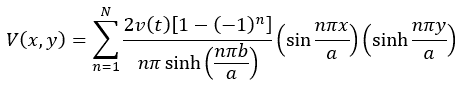
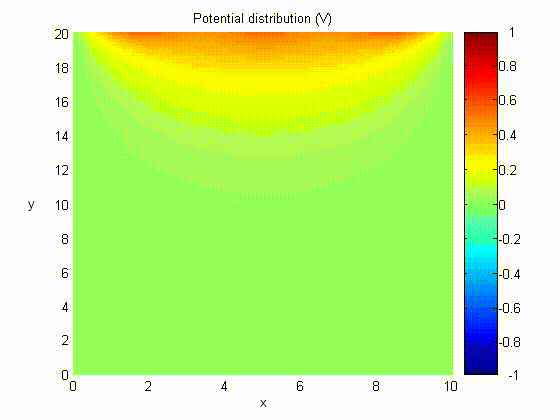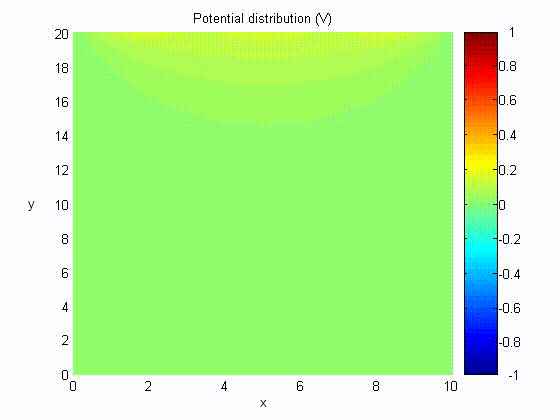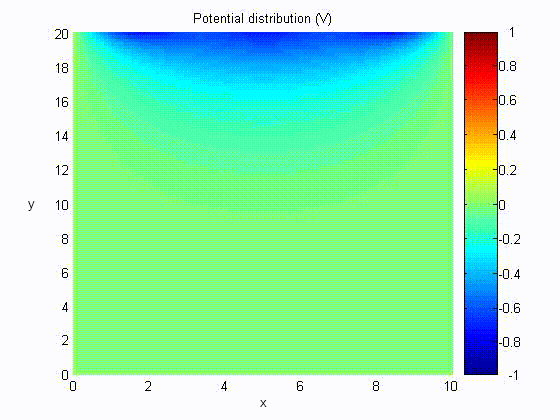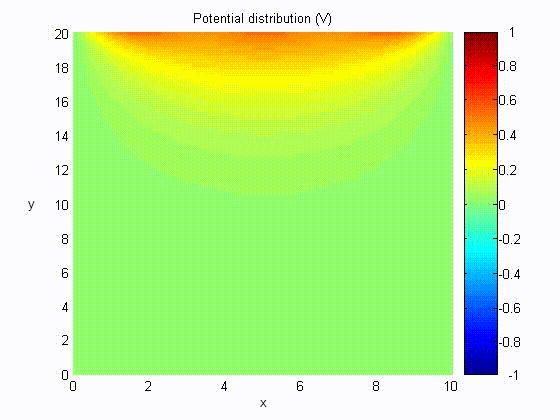
Electric Field Distribution
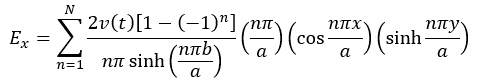
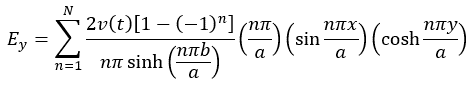
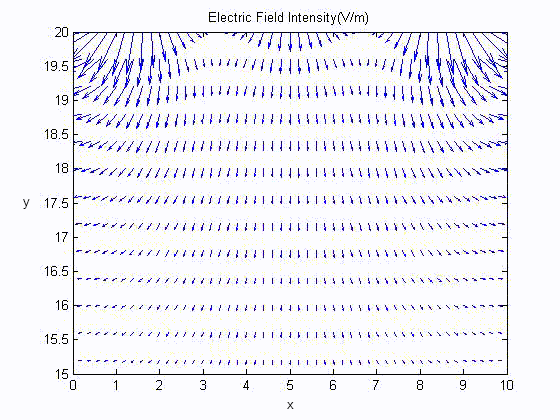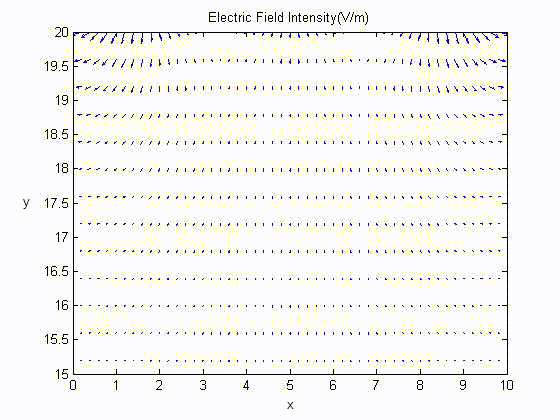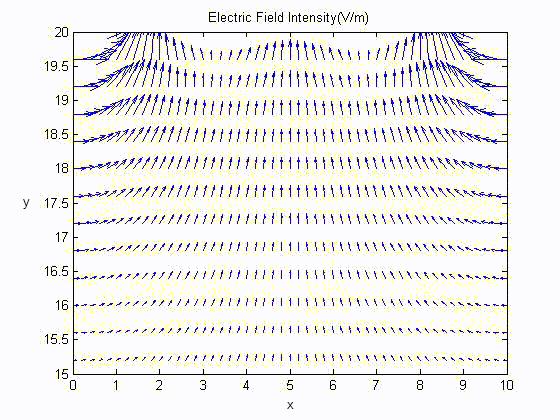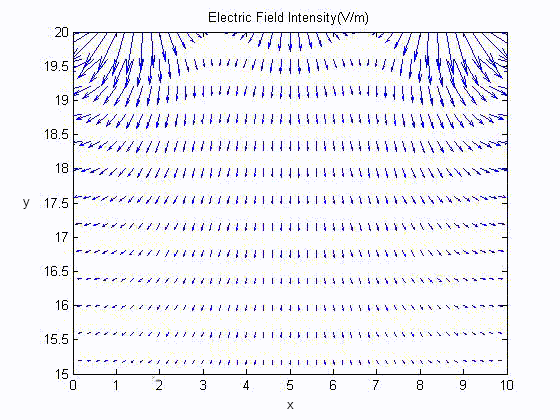
Surface Charge Distribution