Editor: 劉慕德、陳祐融
Advisor: 江簡富
Fig. 1 shows a cylindrical conductor exposed to an external electricfield which approaches \(\hat{x}E_0\) at infinity. The associated boundary condition at infinity becomes \[ \Phi(\rho\to\infty) = -E_0x = -E_0\rho\cos\phi. \]
Properfunctional form of the potential is chosen as \( \Phi = -E_0 \rho \cos \phi + \frac{A}{\rho} \cos \phi \), of which both terms are solutions to the Laplace' equation. Since the potentialon the conductor surface is \( \Phi(\rho = a) = 0\), we have \[ -E_0 a + \frac{A}{a} = 0 \mathrm{\ or\ } A = E_0 a^2. \]

Let \(a=2.5\) and \(E_0 = 1\),
(1) Potential
\[ \Phi_{\mathrm{tot}}(t) = -E_0(t)\rho\cos\phi + E_0(t)a^2\frac{\cos\phi}{\rho}.\ (\mathrm{V})\]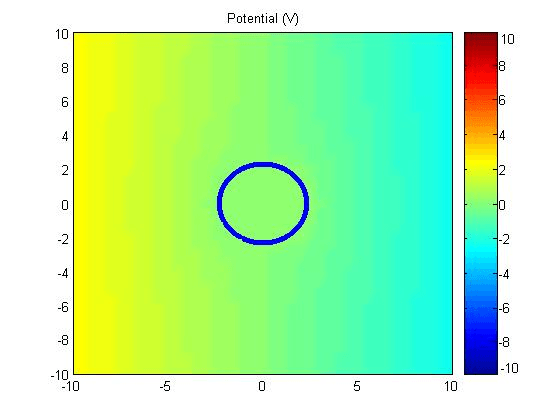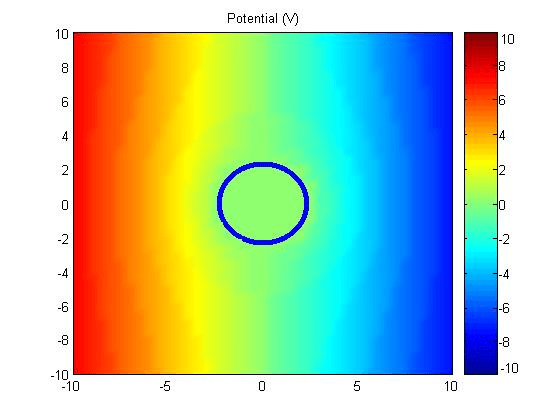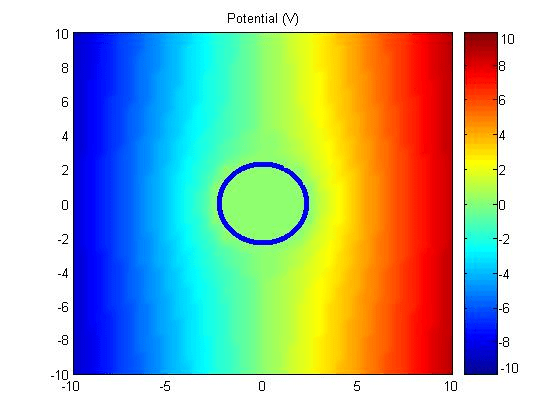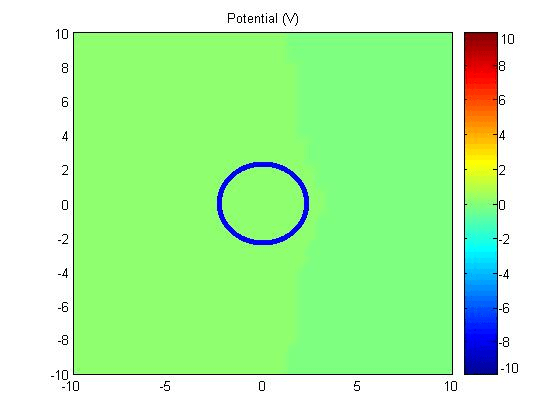
(2) Electric Field and Charge Density
\[ E_{\mathrm{tot}} (t) = \hat{\rho}E_0(t) \left[ 1 + \left(\frac{a}{\rho}\right)^2 \right] \cos \phi + \hat{\phi} E_0 (t) \left[ \left(\frac{a}{\rho}\right)^2 - 1\right] \sin \phi. \ (V/m)\] \[ \rho_s(t) = \varepsilon_0E_0(t) \left[ 1 + \left(\frac{a}{\rho}\right)^2 \right] \cos \phi. \ (C/m^2)\]