MQS Solution with PEC Cylinder Sphere
Editors：楊子毅、呂以德
Adviser：江簡富教授
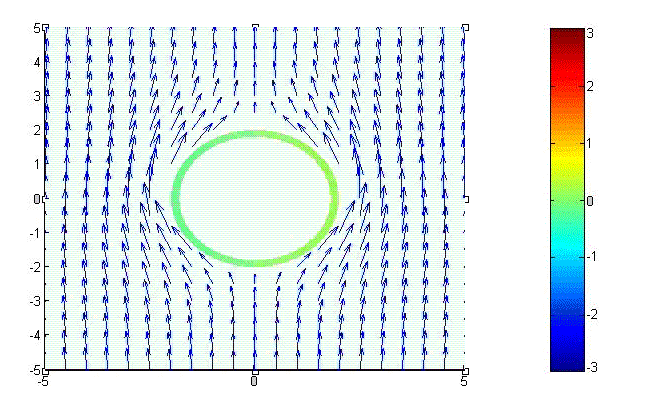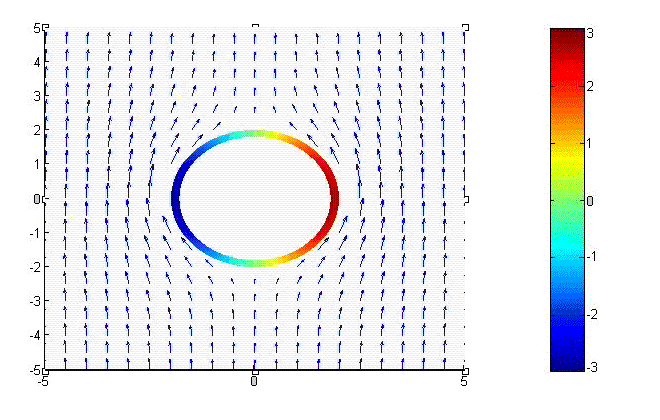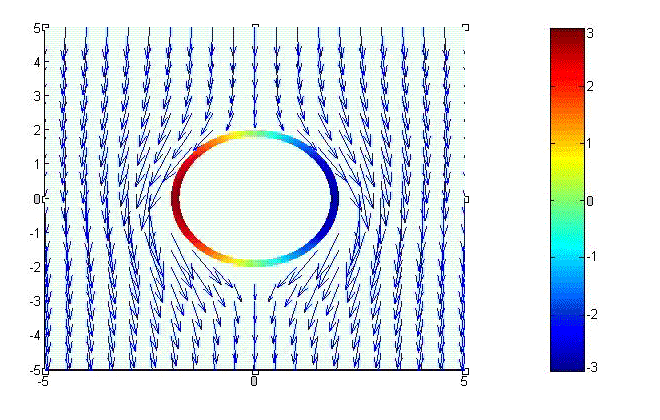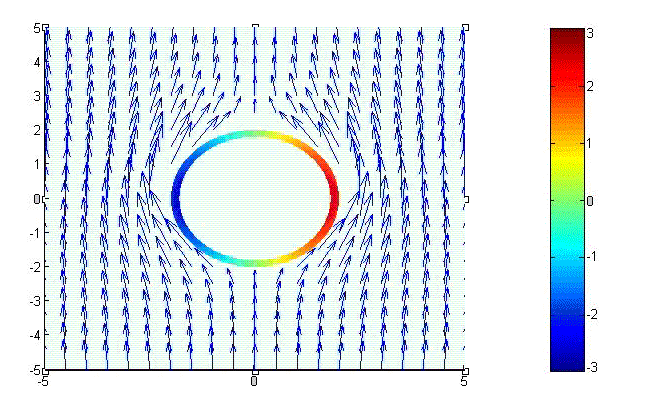
Fig.1 shows a cylindrical conductor exposed to an external magnetic field which approaches \(\hat{x}H_0\) at infinity.
Fig.1 Cylindrical PEC Exposted to An External Magnetic Field
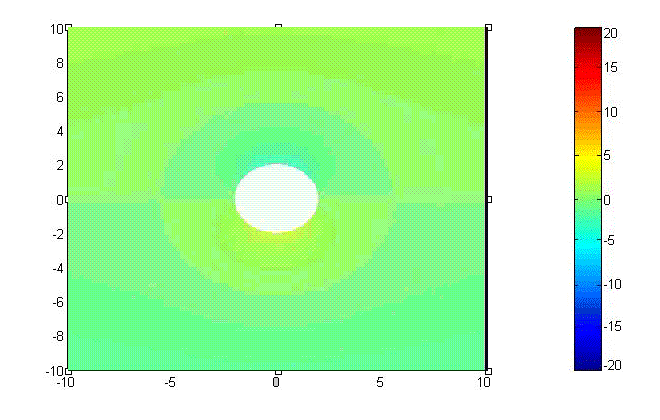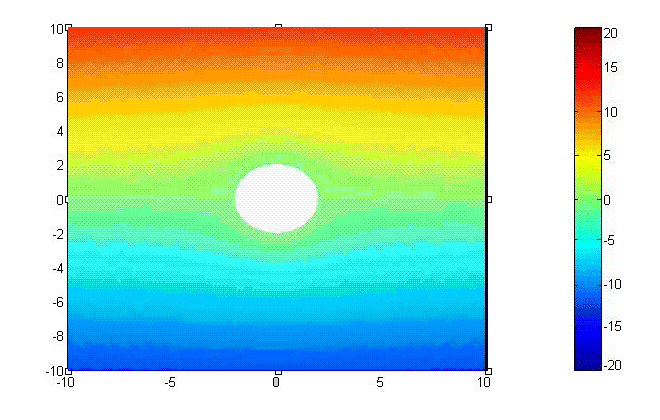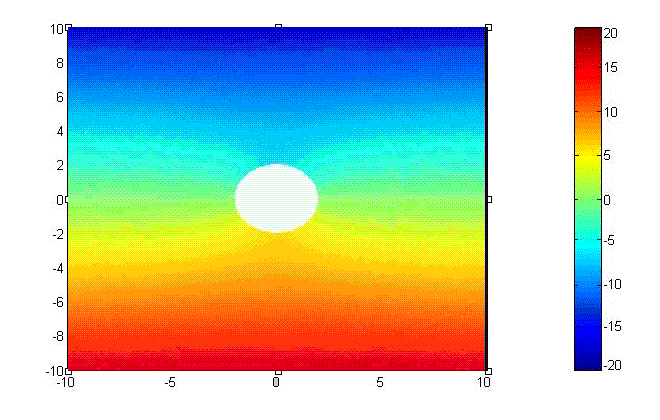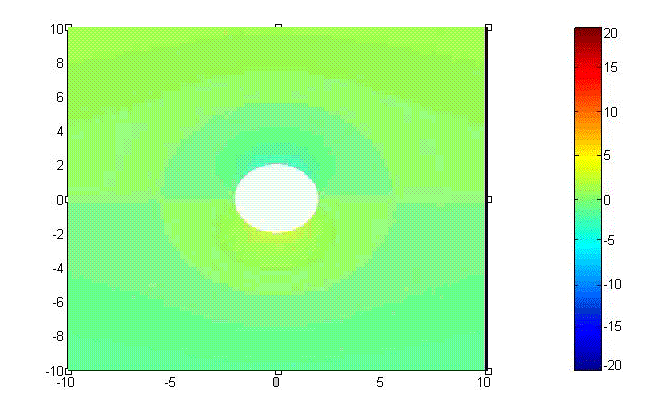
(1)Potential
\[\Phi_{tot\ }=\ -H_0\rho \sin\phi-H_0 a^2\frac{\sin\phi}{\rho}\ \ \ \ \ ({\rm A/m^2})\]
Potential
(2)Intensity
\[H_{tot}=\hat{\rho}H_0 \left( 1- \Bigl({\frac{a}{\rho} \Bigr) }^2 \right) \sin\phi+\hat{\phi}H_0 \left(1+\Bigl({\frac{a}{\rho}\Bigr)}^2 \right)\cos\phi \ \ \ \ \ ({\rm A/m})\] Intensity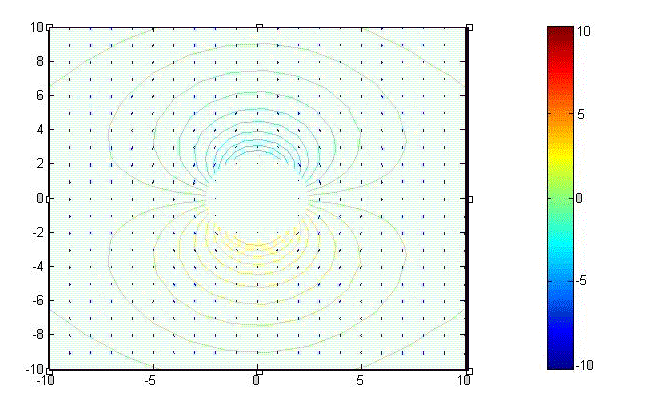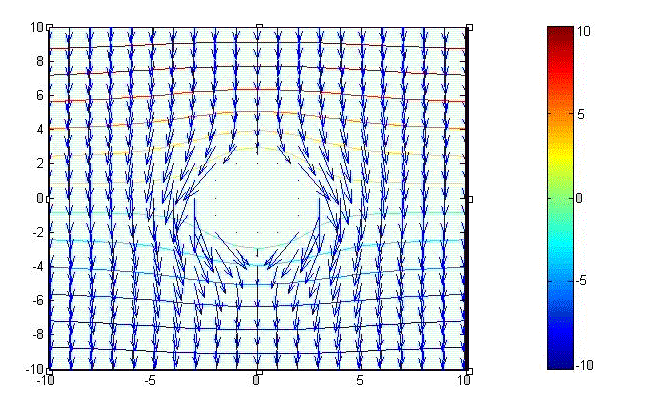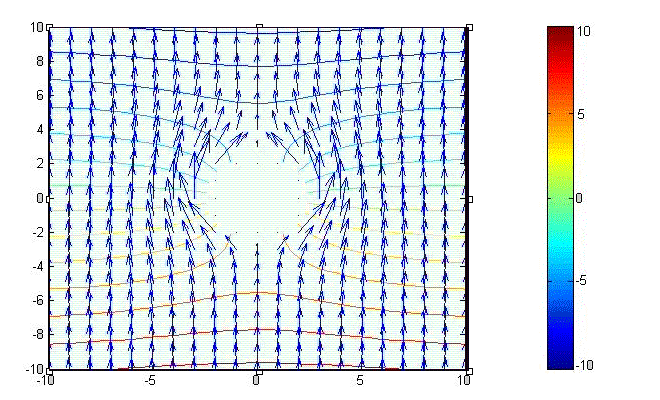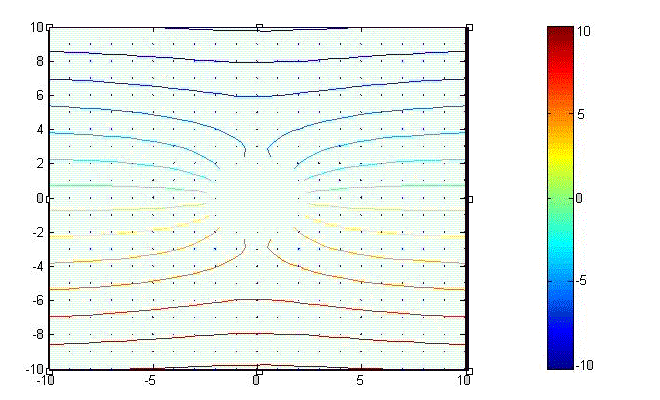
(3)Current Density:
\[J_s=\hat{\rho}\times \left(\bar{H}-0 \right)=H_\phi\hat{z}=2H_0\cos\phi\hat{z}\ \ \ \ \ ({\rm A/m^2})\] Current Density
