MQS Solution with PEC Sphere
Editors :王鐘霆
Advisor:江簡富
教授
![]()
Demonstration:
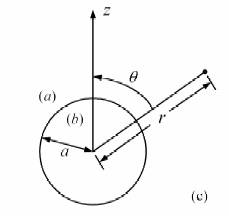
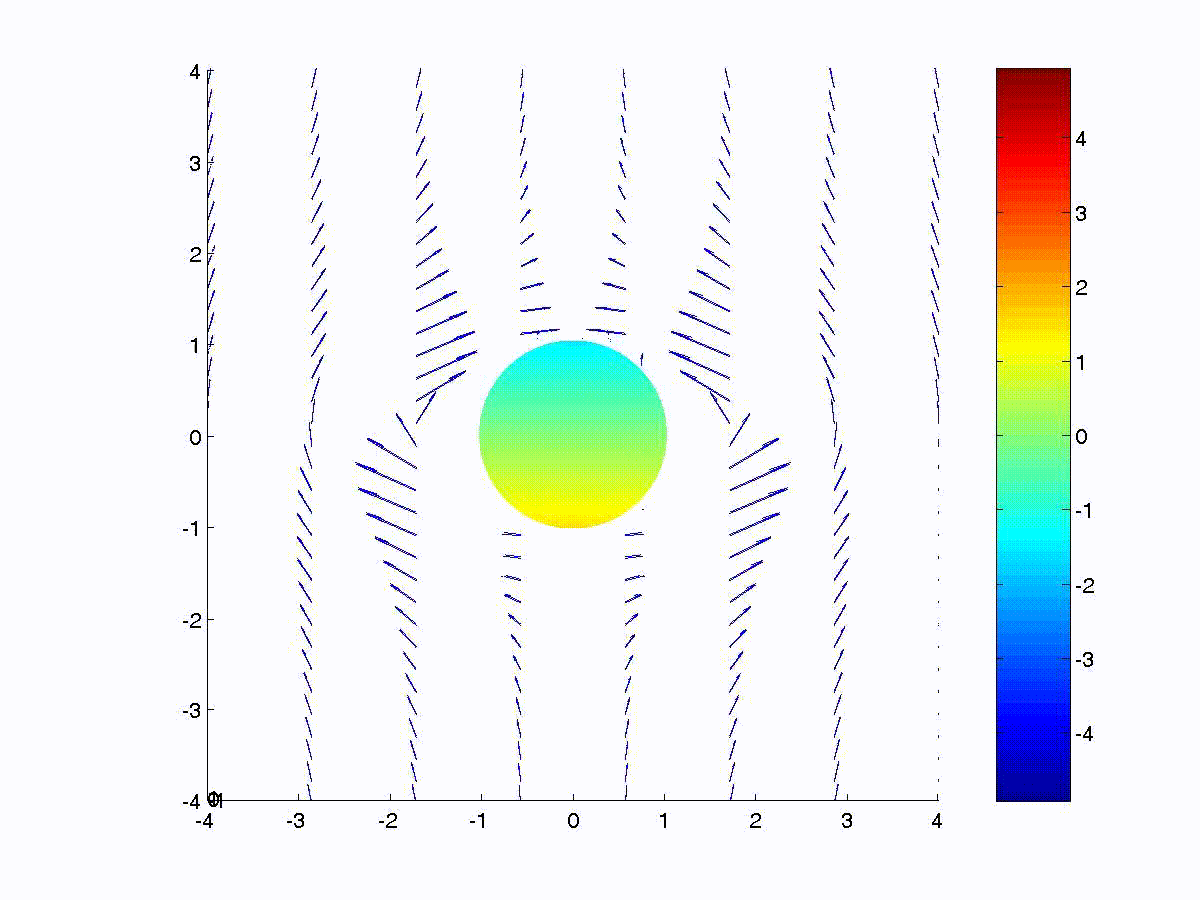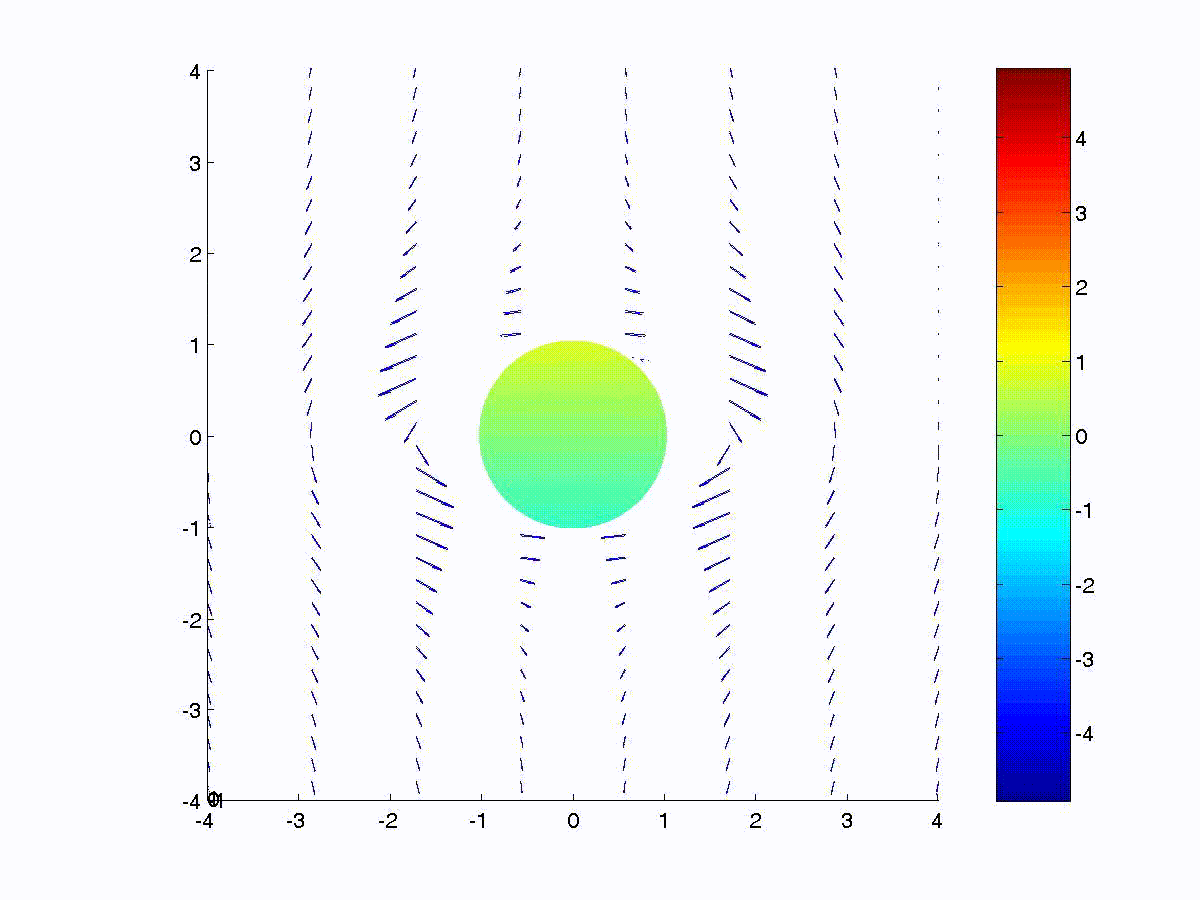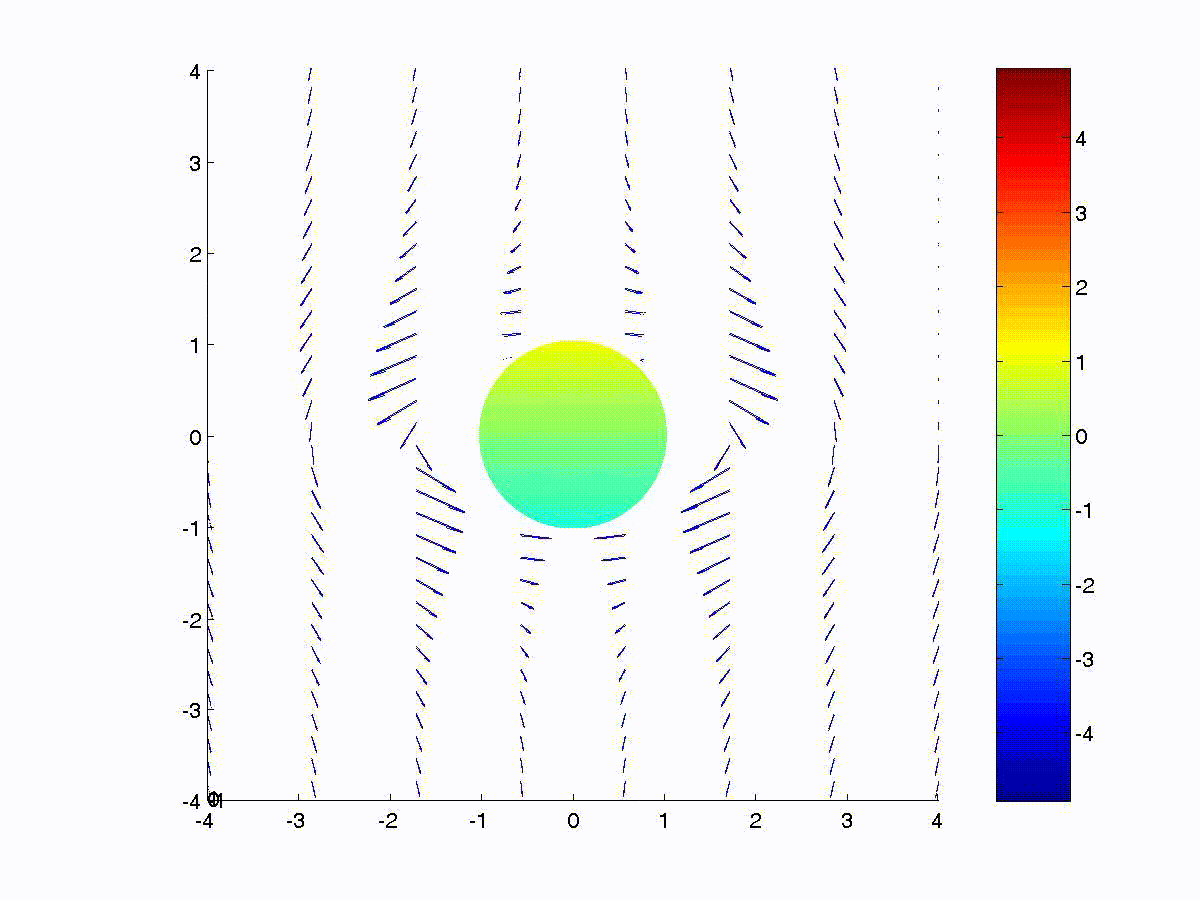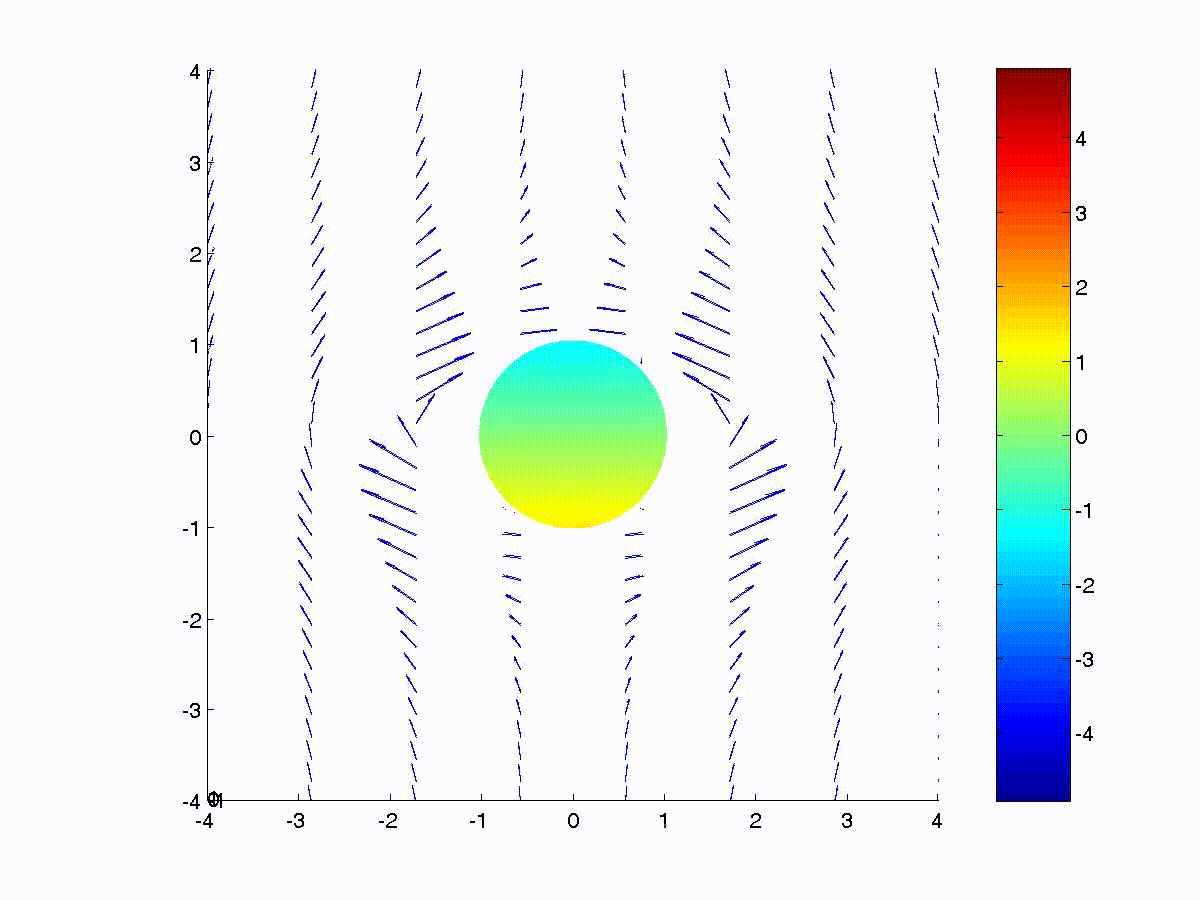
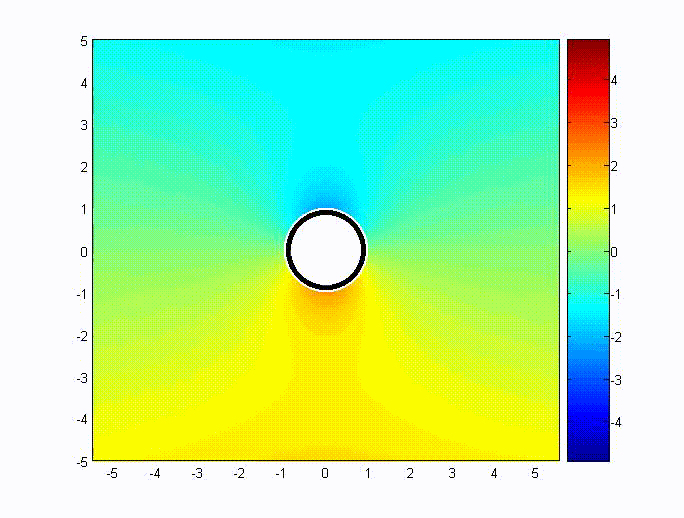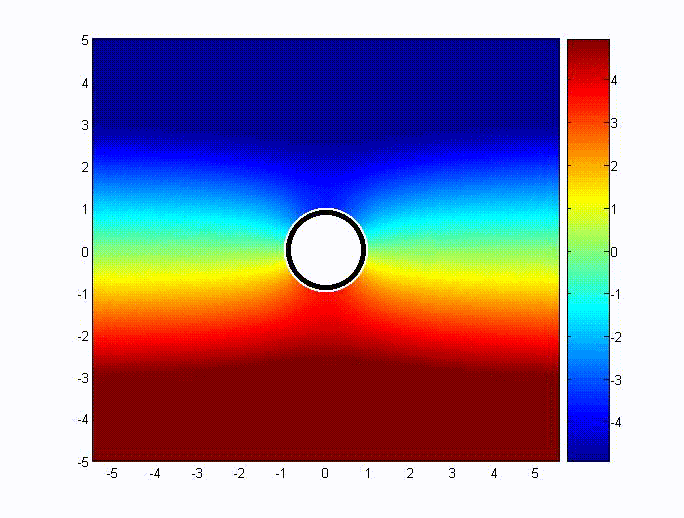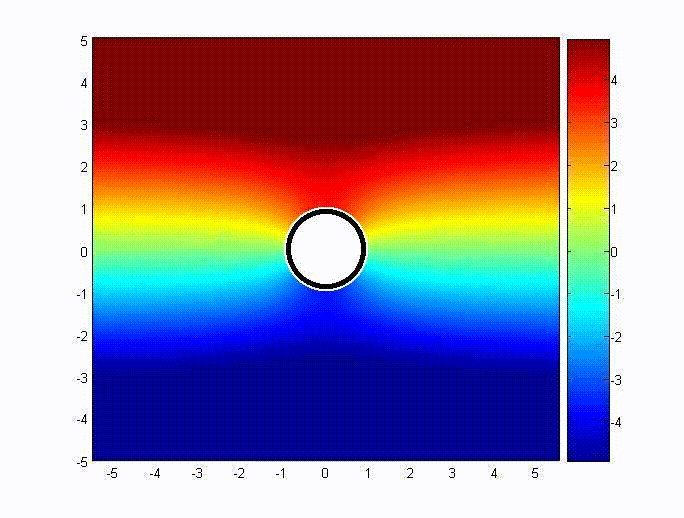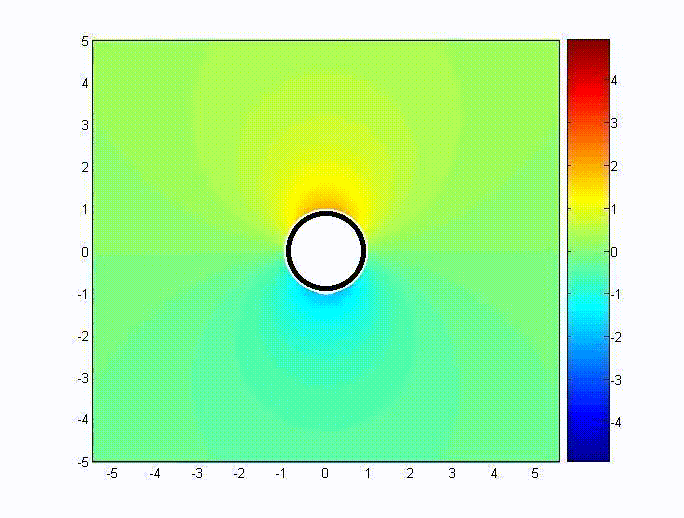
Consider a conductive sphere of radius \(a\) immersed in an applied
external magnetic field, thus \( \mathrm{\bar{H}=\hat{z}H_{0}}\) as \(r\) approaches infinity. The
scalar potential is chosen to be \({\rm\psi=-H_{0}}r\cos\theta+{\rm A}\cos\theta/r^{2}\). Then
the magnetic
field is
\(\mathrm{\bar{H}=-\nabla\psi=H_{0}}\left(\hat{r}\cos\theta-\hat{\theta}\sin\theta\right)+{\rm A}\left(\hat{r}\displaystyle\frac{2\cos\theta}{r^{3}}+\hat{\theta}\displaystyle\frac{\sin\theta}{r^{3}}\right)\)
The boundary condition for \({\rm \mu_{0}}{\rm H}_{r}\left(r=a\right)=0\) gives \({\rm A}=-{\rm H_{0}} a^{3}/2\).
The total magnetic flux passing through a closed contour is related
to its vector potential as
\(\mathrm{\Phi=\iint\limits_S\mu_{0}\bar{H}\cdot d\bar{a}=\iint\limits_S\left(\nabla\times\bar{A}\right)\cdot d\bar{a}=\oint\limits_C\bar{A}\cdot d\bar{\ell}}\)
![]()
![]()