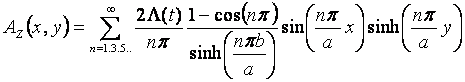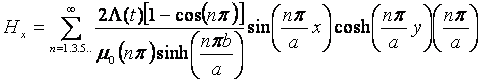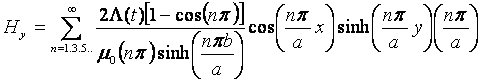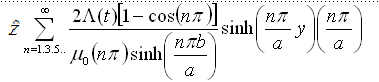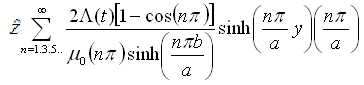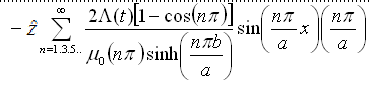MQS
Solution on 2-D Trough
Editors: 趙嘉瀅、林俊宏、張峰嘉
Advisor:
江簡富 教授
Demonstration:
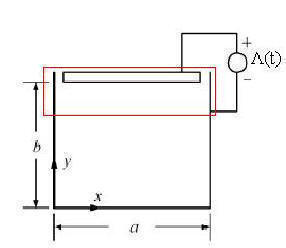
Consider a rectangular trough with the geometry shown in Left Fig. The current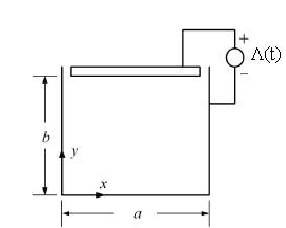
on the side and bottom walls flows in the z direction, and that on the top
wall flows in the −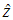 direction.
The vector potential satisfies the Laplace
direction.
The vector potential satisfies the Laplace
equation inside the trough, namely, ▽2Az = 0. The boundary conditions
require that Az(0, y) = Az(a, y) = Az(x, 0) = 0 and Az(x, b) =A
, where
is the total magnetic flux per unit length flowing between the top
wall and the other walls. By MQS approximation:
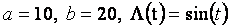
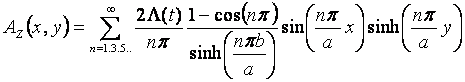
The Biot-Savart low can be derived as follows:
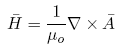
Thus, the magnetic field intensity H in x and y
direction:
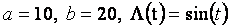
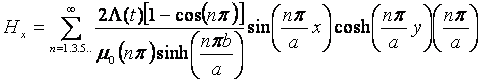
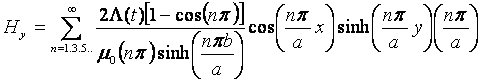
Finally, we simulate the distribution of the surface current Js.From the MQS
approximation.
The Maxwell's equations governing the
magnetic fields are:
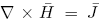
Thus, the surface current Js at boundaries:
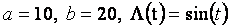
Js at x=0 ,
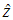 Hy(x=0,y): Hy(x=0,y):
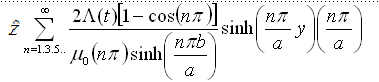 |
Js at x=a ,
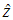 Hy(x=a,y): Hy(x=a,y):
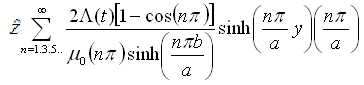 |
Js at y=0 ,
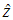 Hx(x,y=0): Hx(x,y=0):
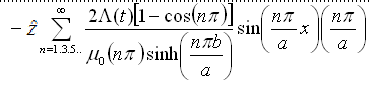 |
Js at y=b ,
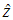 Hy(x,y=b): Hy(x,y=b):
|