Parallel-Plate Waveguide
Editor: 劉志祥 、李宜音 、陳純熙
Adviser: 江簡富教授
The fig shows two parallel plates of width
![]() and
of infinite length, separated by a distance d. one of the wave solution between
these two plates is
and
of infinite length, separated by a distance d. one of the wave solution between
these two plates is
![]()
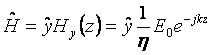
Where ![]() and
and
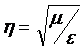 .
At
.
At ![]() and
and
![]() ,
the boundary conditions
,
the boundary conditions ![]() and
and
![]() are
satisfied. The other boundary conditions
are
satisfied. The other boundary conditions
![]() and
and
![]() imply
that
imply
that 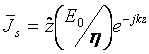 and
and
![]() at
at
![]() ,
,
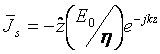 and
and
![]() at
at
![]() .
The current on the bottom plate, I, and the voltage across the two plates, V,
can be defined as
.
The current on the bottom plate, I, and the voltage across the two plates, V,
can be defined as
![]()
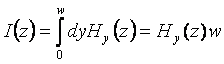 ,
,
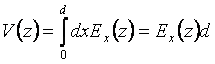
Note that the current on the top plate is of opposite sign with that on the bottom plate, implying that the currents on both plates flow in opposite directions.
Substituting the field expression into the Faraday’s law and Ampere’s law, respectively, we have
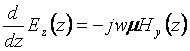
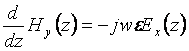
By using the definition in (1.15), (1.16) can be transformed into
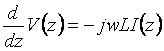
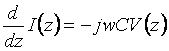
Where ![]() (henry/m),
(henry/m),
![]() (farad/m)
are the per-unit-length inductance and capacitance, respectively, of the
parallel-plate waveguide. Equations (1.17) and (1.18) are called telegrapher’s
equations or transmission line equations, we have
(farad/m)
are the per-unit-length inductance and capacitance, respectively, of the
parallel-plate waveguide. Equations (1.17) and (1.18) are called telegrapher’s
equations or transmission line equations, we have
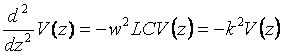 (1.19)
(1.19)
Since ![]() .
The solution to (1.19) are
.
The solution to (1.19) are
![]() ,
,

Where 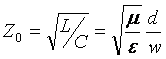 is
the characteristic impedance of the transmission line.
is
the characteristic impedance of the transmission line.
Electric Field Distribution and Surface Charge Distribution
 |
Magnetic Field Distribution and Surface Current Distribution
 |