EQS Solution in Parallel-Wire Line

Authors: Dung-Hao Chen and Yu-Chia Liu

Advisor: Jean-Fu Kiang

Consider an infinitely long, straight-line charge with uniform density of $\rho$ (C/m) along the z-axis. The symmetry of the problem indicates that the potential only depends on the cylindrical coordinate. Thus, by Laplace's equation, we get $$ \nabla^{2} V=0 $$ By symmetry, we know that $$ \frac{\partial}{\partial \phi } =0 \; , \; \frac{\partial}{\partial z } =0 $$ Substitute the above conditions into Laplace's equation, we get $$ \frac{1}{r} \frac{\partial }{\partial r} \left ( r\frac{\partial V}{\partial r} \right ) =0 $$ By solving the Differential equation, we get a general solution. $$ V=A\ln r+B $$ Using the relationship between electric field and voltage, we get $$ \bar{E}=-\nabla V= -\hat{r} \frac{\partial V}{\partial r}= -\hat{r} \frac{A}{r} $$ Using Gauss' Law, we can find $A$. $$ \int \int \bar{D} \cdot d\bar{a}=Q \Longrightarrow -\frac{\epsilon A}{r} 2\pi r \ell=\rho \ell \Longrightarrow A=\frac{-\rho }{2\pi \epsilon } $$ Substitute it back to the general solution of $V$, and let $r=r_{0}$ be the place where the voltage is $0$, so that $B=\frac{\rho }{2\pi \epsilon }\ln r_{0}$ , and we get $$ V=\frac{-\rho }{2\pi \epsilon }\ln r+\frac{\rho }{2\pi \epsilon }\ln r_{0}=\frac{-\rho }{2\pi \epsilon }\ln \frac{r}{r_{0} } $$ 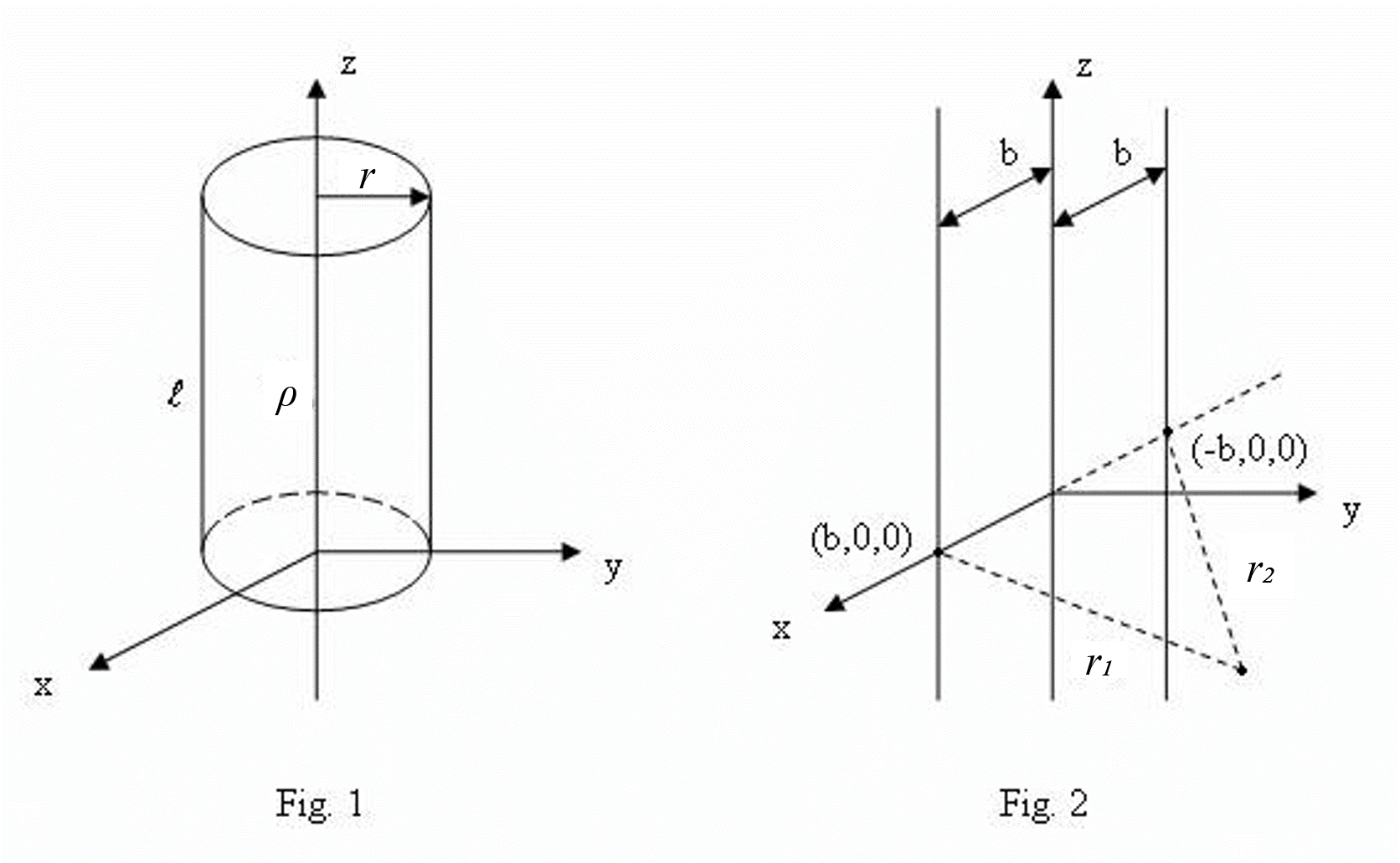When two infinitely long, straight-line charges of equal and opposite uniform charge densities $\rho $ and $-\rho $, respectively, parallel to the z-axis and passing through $(b,0,0)$ and $(-b,0,0)$, respectively. And by changing Cylindrical coordinate to Cartesian coordinate: $$ \hat{r}=\frac{\hat{x}x+\hat{y}y}{\sqrt{x^{2}+y^{2} } } $$ We get the electric field in Cartesian coordinate. $$ \bar{E}= -\hat{r} \frac{A}{r} =A \; \frac{-\hat{x}x-\hat{y}y }{\sqrt{x^{2}+y^{2}} } \; \frac{1}{\sqrt{x^{2}+y^{2}}} =A \; \frac{(-\hat{x}x-\hat{y}y)}{x^{2}+y^{2}} $$ By shifting the result of the previously derived formula of $\bar{E}$, from $(0,0,0)$ to $(b,0,0)$, then we can get the electric field contributed by the positively charged wire. $$ \bar E_{pos}=A \; \frac{-\hat{x}( x-b )-\hat{y}y} {( x-b ) ^{2} +y^{2}} $$ Likewise, we can also derive the electric field contributed by the negatively charged wire. $$ \bar E_{neg} =( -A )\frac{-\hat{x}( x+b )-\hat{y}y }{ ( x+b ) ^{2} +y^{2}} $$ Finally, by superposition, we get the total electric field in Cartesian coordinate. 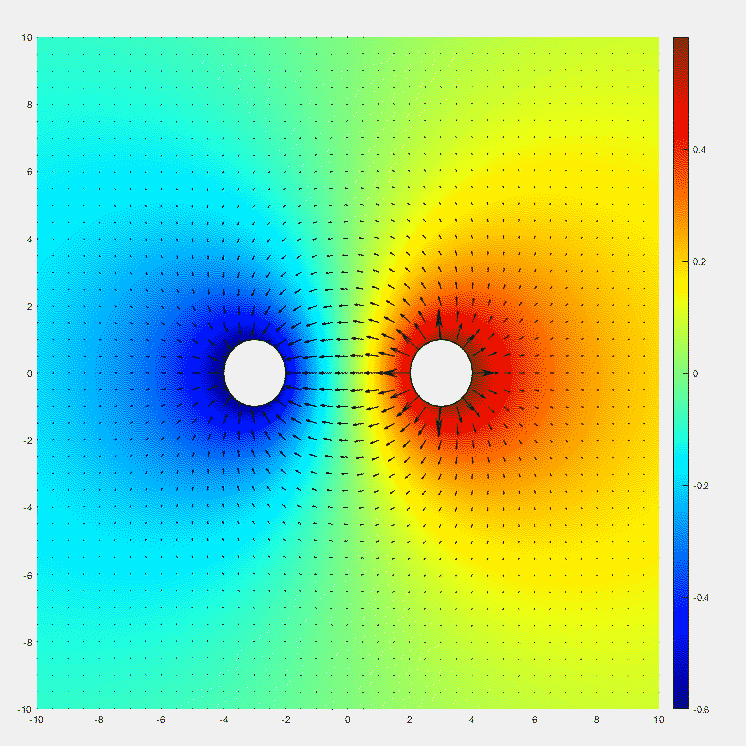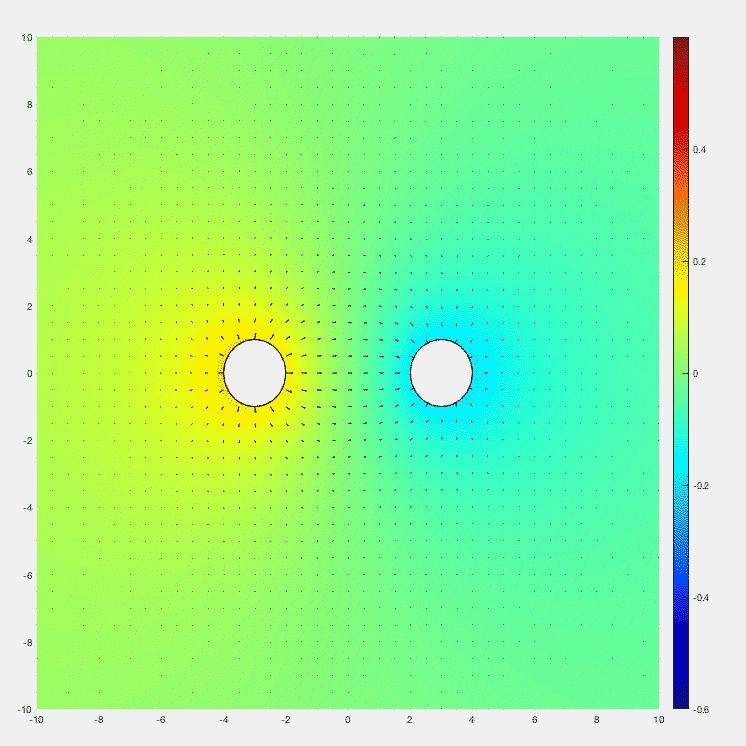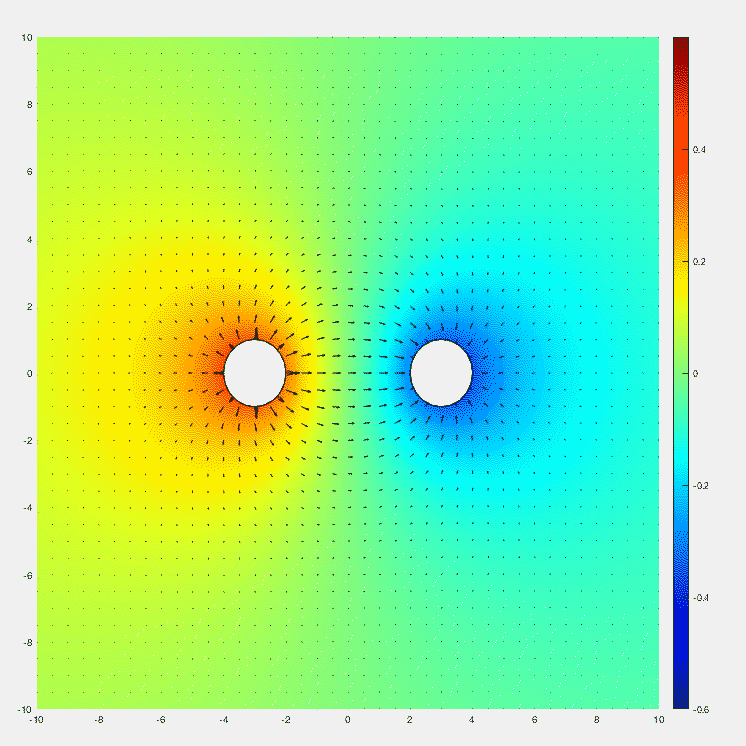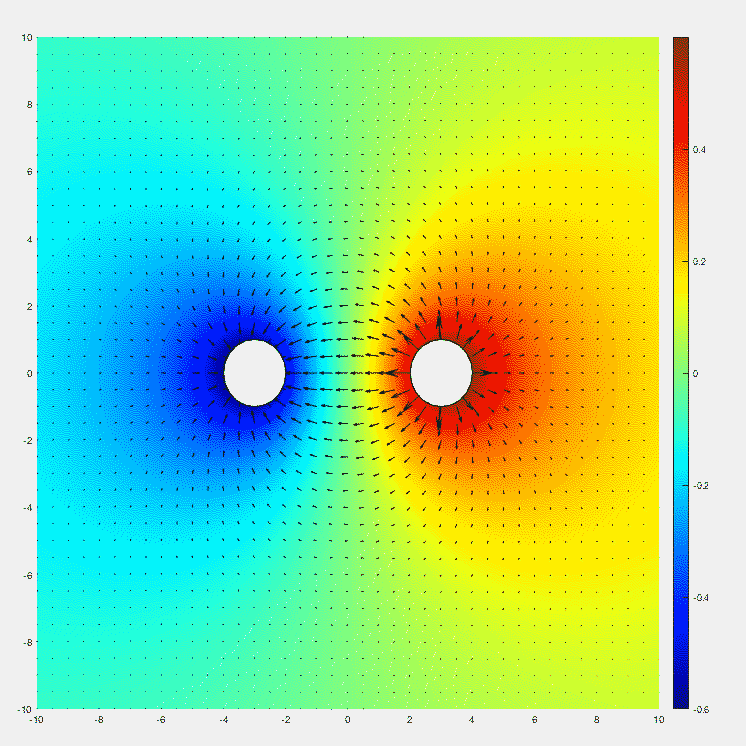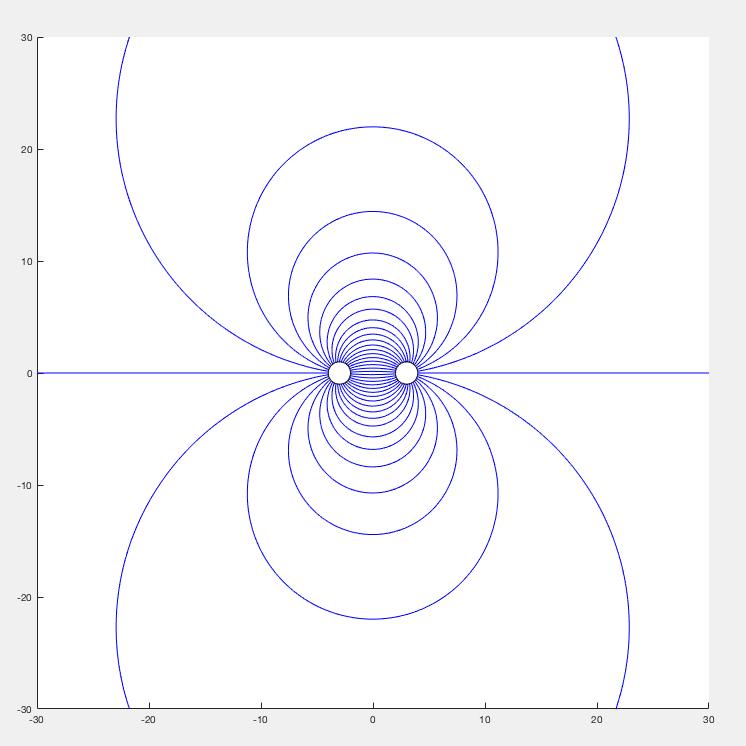$$ \bar E_{total}=\bar E_{pos}+\bar E_{neg} $$ $$ =\hat{x} A\left [ \frac{- ( x-b )}{ ( x-b ) ^{2} +y^{2}} +\frac{x+b}{ ( x+b ) ^{2} +y^{2}} \right ] $$ $$ + \hat{y} A\left[ \frac{-y}{ ( x-b ) ^{2} +y^{2}}+\frac{y}{ ( x+b ) ^{2} +y^{2}} \right] $$ Note that there is no electric field inside both parallel-wire lines. To obtain the EQS solution, simply change $\rho $ to $\rho \cos \left ( \omega t \right ) $, which is a time-harmonic. Now, let's take a look at the voltage. Let the distance between the point of interest and the positively charged wire be $r_{1}$, and the distance between the point of interest and the negatively charged wire be $r_{2}$. By superposition, the potential due to the two line charges is $$ V=\frac{-\rho }{2\pi \epsilon } \ln \frac{r_{1} }{r_{01}} +\frac{-\rho }{2\pi \epsilon } \ln \frac{r_{2} }{r_{02}} $$ Where $r_{01}$ and $r_{02}$ are the distances from the line charges to the reference point at which the potential is zero. By choosing the reference point to be equidistant from the two line charges, we have $r_{01}=r_{02}$. And the equipotential surface for the potential field is given by $$ V=\frac{-\rho }{2\pi \epsilon } \ln \frac{r_{2} }{r_{1}} $$ In order to find the equipotential surface, we first let $\frac{r_{2} }{r_{1}}$ be a constant $k$. Then, by expressing $r_{01}$ and $r_{02}$ by Cartesian coordinate, we can get $$ \frac{( x+b ) ^{2} +y^{2} }{ ( x-b ) ^{2} +y^{2} } =k^{2} $$ $$ \Longrightarrow x^{2} +2bx+b^{2} +y^{2} =k^{2} ( x^{2} -2bx+b^{2} +y^{2}) $$ $$ \Longrightarrow ( k^{2}-1 ) ( x^{2}+y^{2}+b^{2} ) - ( k^{2}+1 ) 2bx=0 $$ $$ \Longrightarrow \left ( x-b\frac{k^{2}+1}{k^{2}-1} \right ) ^{2} +y^{2}=\left ( b\frac{2k}{k^{2}-1} \right ) ^{2} $$ So the equipotential surfaces are the cylindrical surfaces. Their center line of the cylindrical pass through $(b\frac{k^{2}+1}{k^{2}-1},0,0)$ on the xy-plane, and the radius of the cylindrical are $\left | b\frac{2k}{k^{2}-1} \right | $, where $k\ge 0$. Notice that when $k=1$, the equipotential surface degenerates to a plane, which is $x=0$.