EQS Solution in Parallel-Wire Line

Editor：張祖恩、張凱崴、曾冠傑

Advisor：江簡富 教授

Demonstration

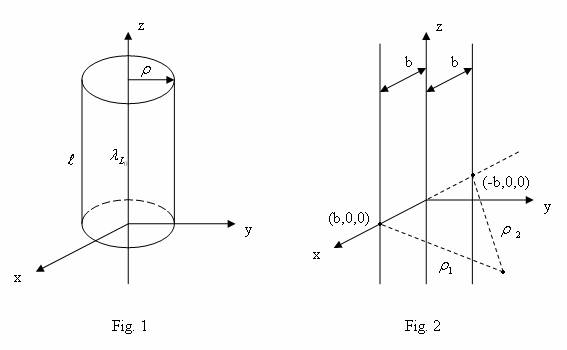
Consider an infinitely long, straight-line charge with uniform density of C/m along the z-axis, as shown in Fig.1. The symmetry of the problem indicates that the potential only depends on the cylindrical coordinate . Thus, we have

where A and B are constants to be determined. Set the potential arbitrarily to be zero at a reference . Thus, and

Apply the electric Gauss’ law to the cylindrical tube in Fig.1 to have

Thus, we have and

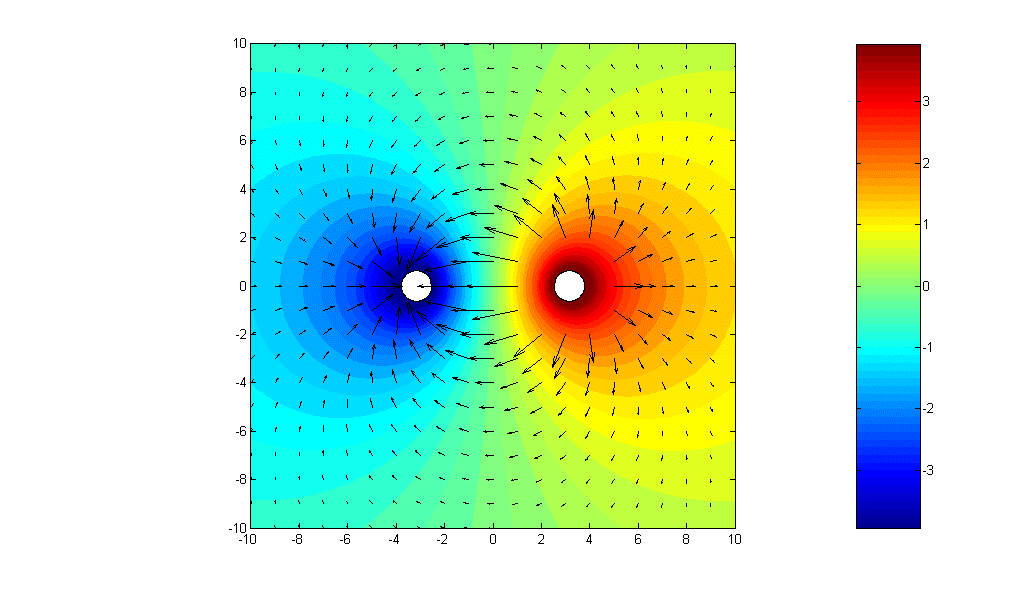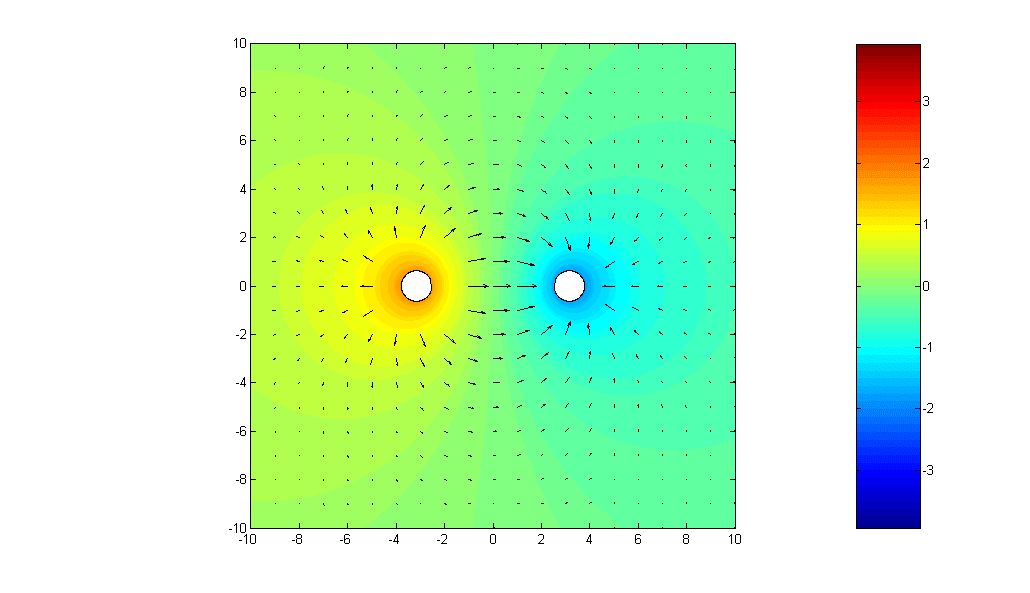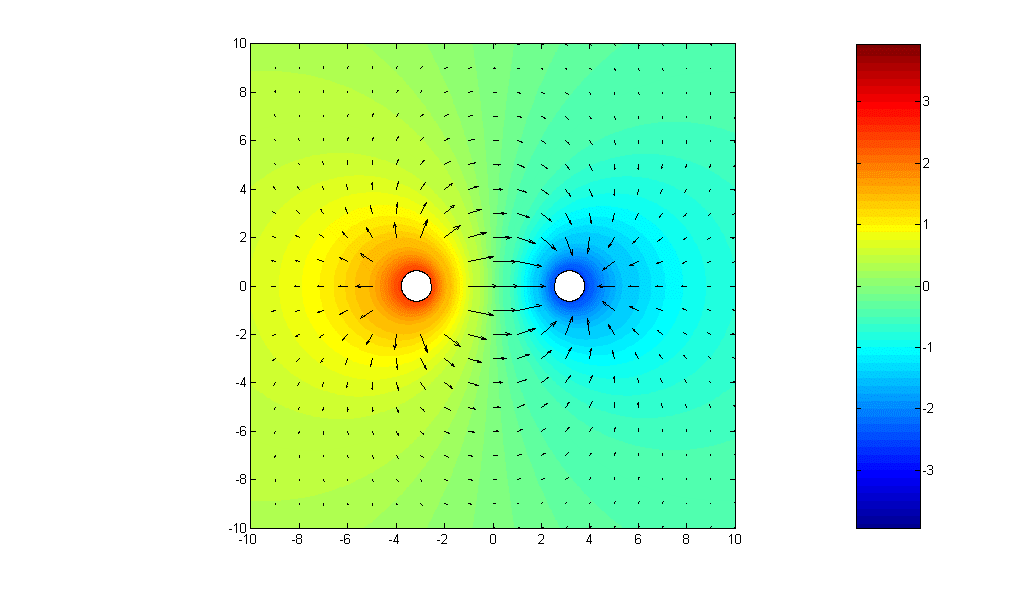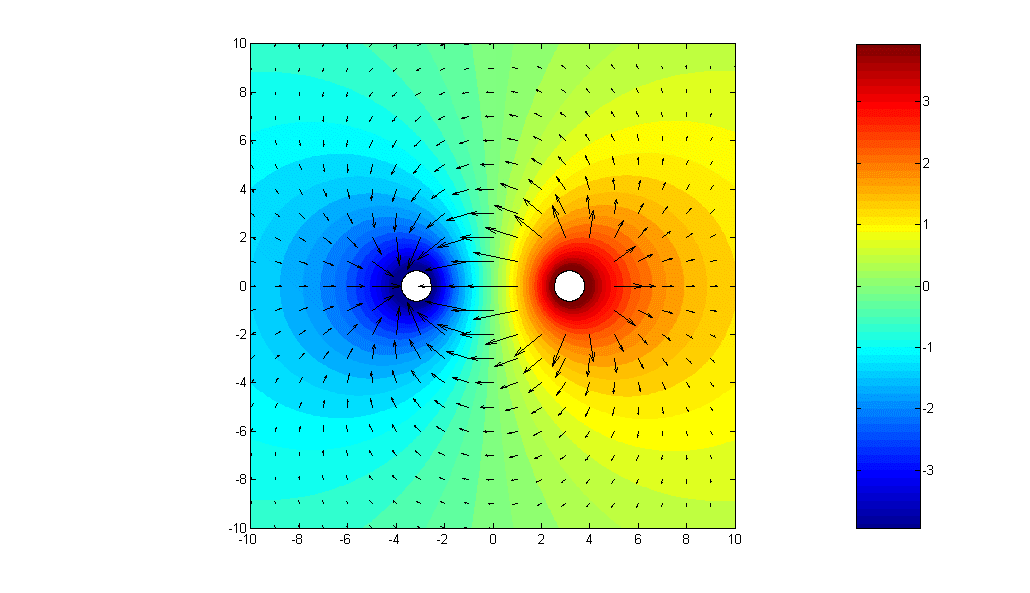
Next, Fig.2 shows two infinitely long, straight-line charges of equal and opposite uniform charge densities C/m and C/m, respectively, parallel to the z-axis and passing through and , respectively. By superposition, the potential due to the two line charges is

where and are the distances from the point of interest to the line charges, and are the distances from the line charges to the reference point at which the potential is zero. By choosing the reference point to be equidistant from the two line charges, we have , and

The equipotential surface for the potential field is given by

where k is a constant lying between 0 to ∞.The equipotential surface in the Cartesian coordinates can be expressed as

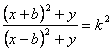
or

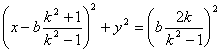
The associated potential of the equipotential surface is

Note that there is no electric field inside both parallel-wire lines.

To obtain the EQS solution, simply change to , which is a time-harmonic.

Choose =2 C/m, b=3 m, radii of the wires = 0.3 m