Transmission Line
Connected with a Nonlinear Load
Authors: 陳品諺、李佾儒
Advisor: 江簡富教授
Load-line
technique is a graphical technique frequently used to analyze the voltage and
current along a transmission line connected with a nonlinear load.
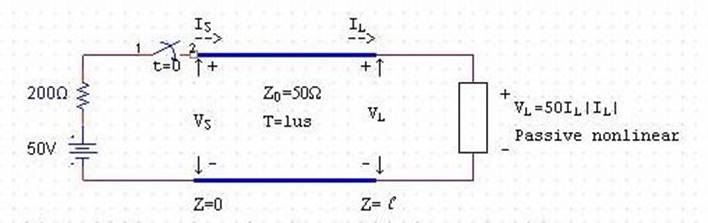
Fig.1:
Transmission line terminated by a passive nonlinear element and driven by a
constant voltage source in series with a resistance.
Fig.1
shows a transmission line terminated by a passive nonlinear element having the I-V relationship of![]() , and the source
end is consisted of a resistor of 200Ω
and a dc voltage of 50V. The
characteristic impedance of the transmission line is
, and the source
end is consisted of a resistor of 200Ω
and a dc voltage of 50V. The
characteristic impedance of the transmission line is![]() , and the
transverse time along the line is
, and the
transverse time along the line is![]() . The switch S is
closed at
. The switch S is
closed at![]() , and the
load-line technique is used to obtain the time variation of the voltages
, and the
load-line technique is used to obtain the time variation of the voltages ![]() and
and ![]() at the source and at the load ends,
respectively.
at the source and at the load ends,
respectively.
The Kirchhoff voltage law at![]() implies
implies
![]()
At
![]() ,
,
![]()
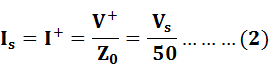
![]() and
and
![]() are
the voltage and current, respectively, of the (+) wave propagating in +z direction
immediately after closure of the switch. We can solve
are
the voltage and current, respectively, of the (+) wave propagating in +z direction
immediately after closure of the switch. We can solve ![]() and
and
![]() graphically
by drawing two straight lines to represent (1)
and (2) as shown in Fig.2. The point of intersection is
denoted by A, which gives the values of
graphically
by drawing two straight lines to represent (1)
and (2) as shown in Fig.2. The point of intersection is
denoted by A, which gives the values of ![]() and
and![]() .
.
![]()
![]()
![]()
![]()
![]() When the (+) wave reaches the load end
When the (+) wave reaches the load end![]() at
at![]() , a (-)
wave is induced, the voltage and current at
, a (-)
wave is induced, the voltage and current at![]() at
at![]() can be expressed a
can be expressed a
![]()
![]()
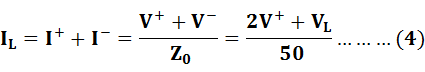
where
![]() and I- are the (-) wave voltage and current,
respectively. The solution of
and I- are the (-) wave voltage and current,
respectively. The solution of ![]() and
and ![]() is given by the intersection of
the curve representing (3) and the
straight line representing (4), the
intersection is denoted by B.
is given by the intersection of
the curve representing (3) and the
straight line representing (4), the
intersection is denoted by B.
When
the (-) wave reaches the source end![]() at
at![]() , another reflection is induced, denoted
as (-+) wave.
, another reflection is induced, denoted
as (-+) wave.
The voltage and current at![]() and
and![]() satisfies the same KVL:
satisfies the same KVL:
![]()
The
voltage and current are consisted of
![]()

where ![]() and
and ![]() are the (-+) wave voltage and current, respectively. Note that
are the (-+) wave voltage and current, respectively. Note that ![]() and
and ![]() is a solution to (5), implying that the straight line representing (6) passes through B. Thus, the solution of (5)
and (6) is given by point C in Fig.2.
is a solution to (5), implying that the straight line representing (6) passes through B. Thus, the solution of (5)
and (6) is given by point C in Fig.2.
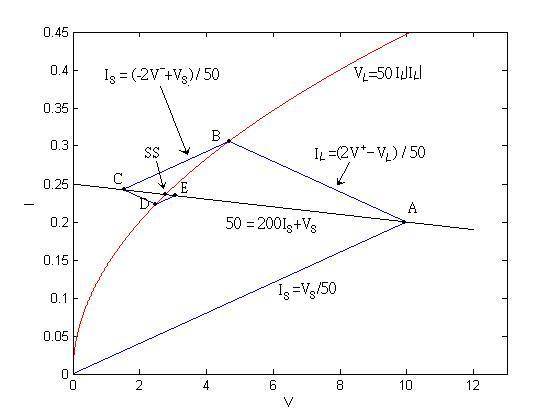
Fig.2: Graphical representation of voltage and current waves.
Continuing this process, we observe that the solutions at![]() are the points of intersection of either
the source or the load V-I curve
with the straight lines of slope
are the points of intersection of either
the source or the load V-I curve
with the straight lines of slope ![]() or
or![]() , respectively. The first straight line
launches at the origin and the following straight line originates at the
previous point of intersection. To be more specific, solutions of
, respectively. The first straight line
launches at the origin and the following straight line originates at the
previous point of intersection. To be more specific, solutions of ![]() and
and
![]() are obtained by drawing the
intersection of the straight lines of slope
are obtained by drawing the
intersection of the straight lines of slope ![]() and (1), whereas that of
and (1), whereas that of ![]() and
and ![]() are obtained by drawing the
intersection of the straight lines of slope
are obtained by drawing the
intersection of the straight lines of slope ![]() and (3), originating from A,
and so on.
and (3), originating from A,
and so on.
Once we have the time variations of ![]() and
and
![]() ;
;![]() and
and![]() , the voltage and current at an
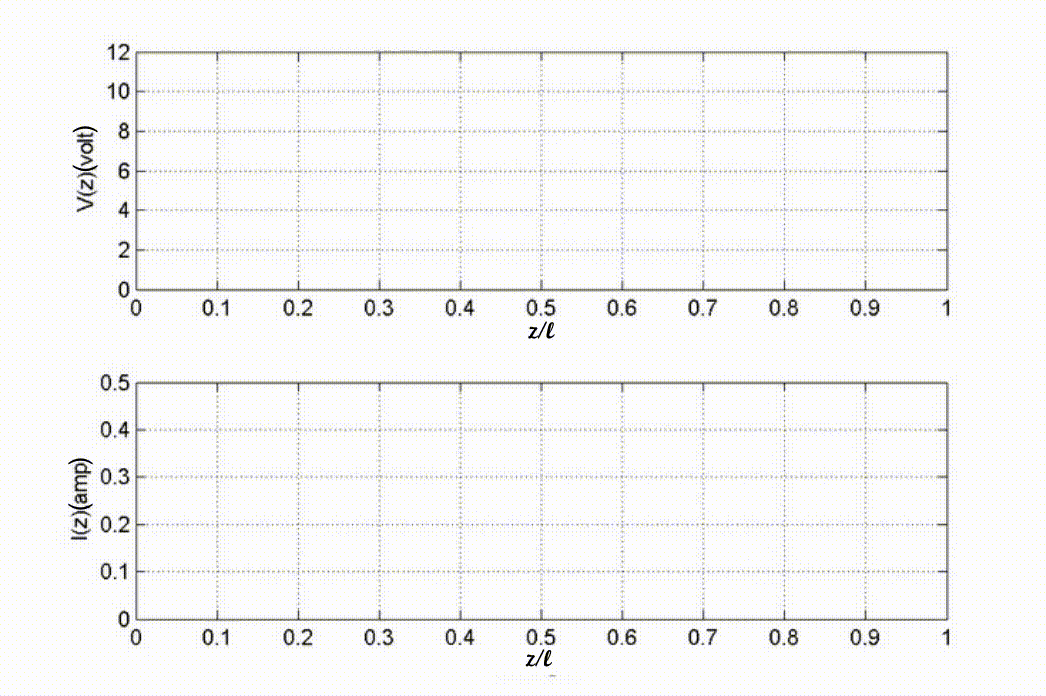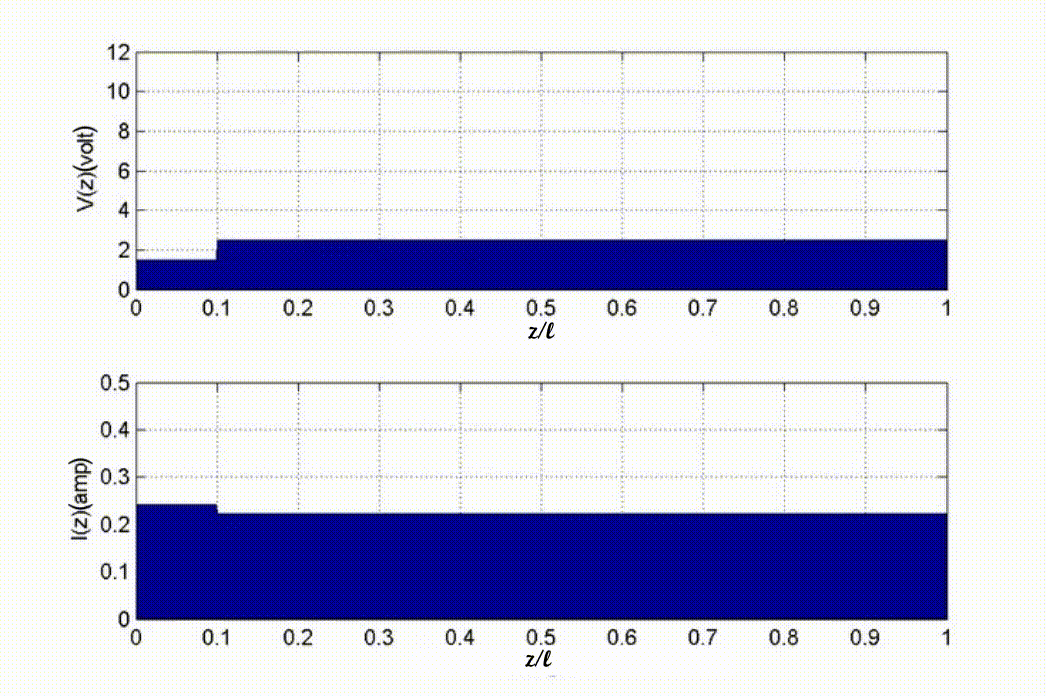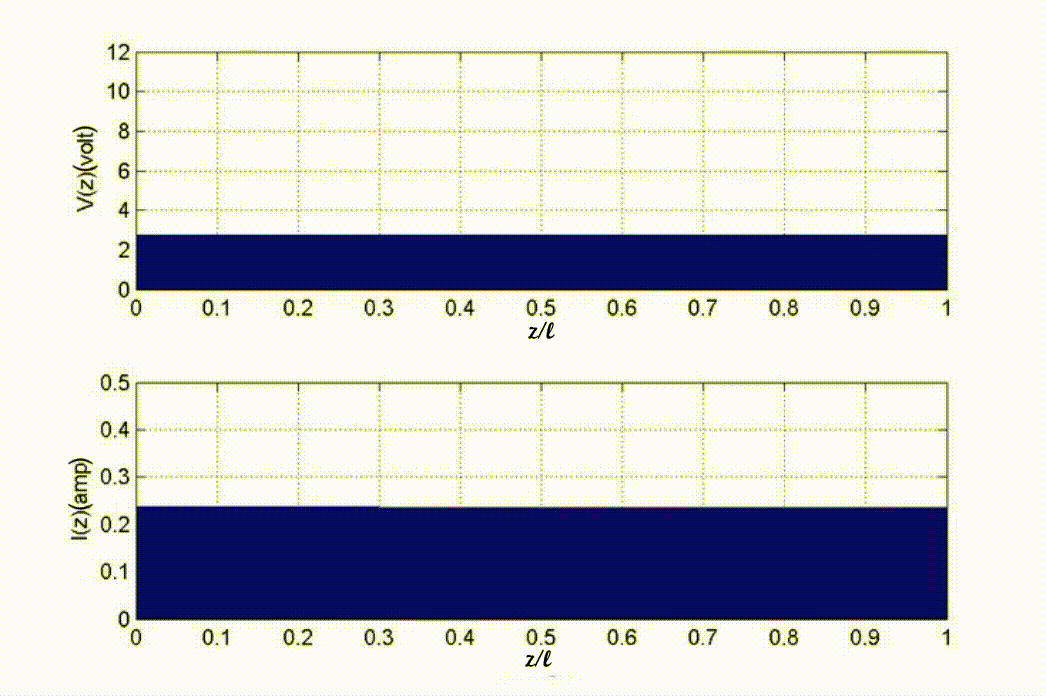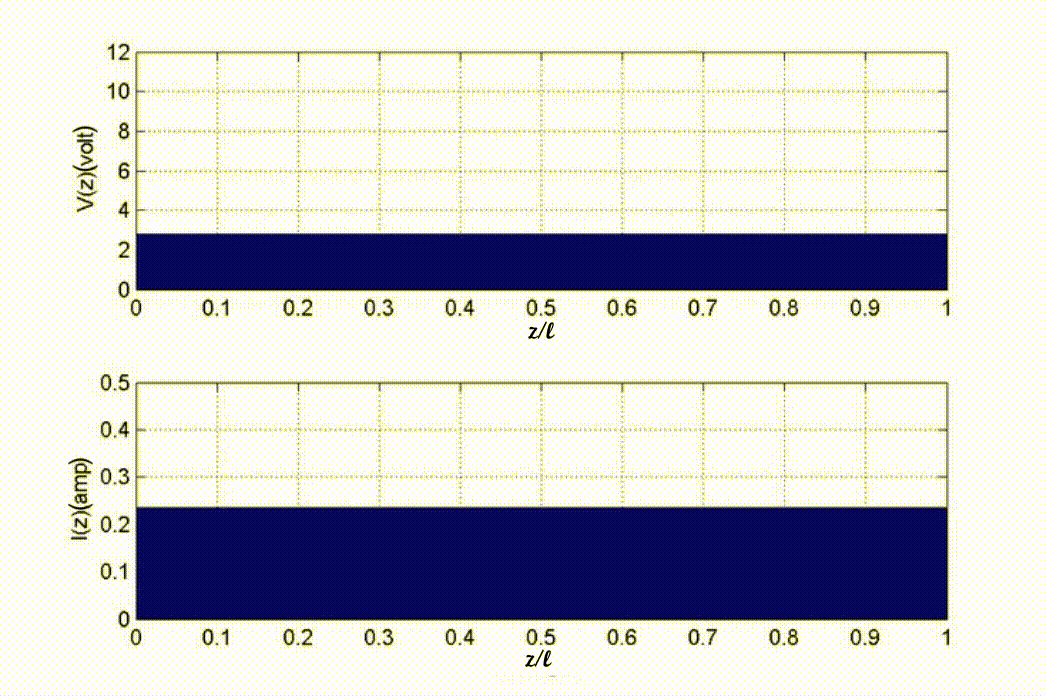
arbitrary point on the transmission line at time t can be obtained. Consider
the following example. When
, the voltage and current at an
arbitrary point on the transmission line at time t can be obtained. Consider
the following example. When![]() at
at![]() , the voltage and current should be
equal to that at the load end when
, the voltage and current should be
equal to that at the load end when![]() . On the other hand, at the same time,
at
. On the other hand, at the same time,
at![]() , the (-) wave has not yet traveled to this point, hence the voltage and
current is equal to that at the source end when
, the (-) wave has not yet traveled to this point, hence the voltage and
current is equal to that at the source end when![]() .
.