Single Stub Matching
Editor:張宏彬
Advisor:江簡富
(I) Analytic Approach
where n is
an integer (positive or negative). The amplitude and
phase of 
are
The parameter 
and 
can be expressed in terms of 
and 
as
(1)
(2)
Two possible solutions for b and ds
are given in (1) and (2) respectively, where the integer value for n
is chosen such that 
.
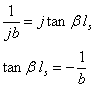
(II) Smith Chart Approach
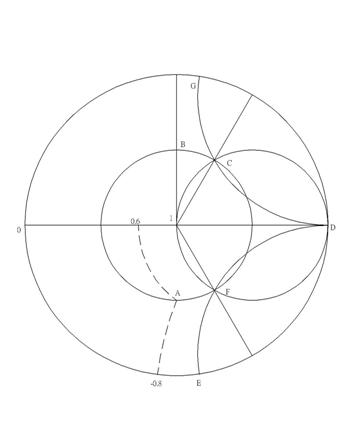
(a) 
=> point A
(b) Drawing constant SWR circle passing through A, go around the
constant SWR circle by half a revolution to B which corresponds to 
(c) The constant SWR is also the locus of 
. Draw r = 1 circle and find C
and F which correspond to two solutions of . The distance moved from B to C is the
location of stub.
(d) Since the short circuit corresponds to a susceptance of infinity, we start at point D
(the outmost
circle) to reach E which is the input admittance of the stub normalized with
. The distance moved
from D to E is the length of the stub.
(e) The second solution of can be obtained from
(c), which is the distance moved
from B to F.
(f) The second solution of 
can be obtained from (d).where is the distance from
D to G.
Parameter in DEMO：
，
=>
The general expressions for the line voltage and line current are
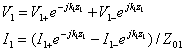
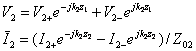
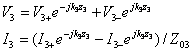
the waves satisfy the boundary condition given by：
(1) at 
=0
, 
(2) at 
=0
, 
(3) at 
=0
, 
(4) (5) at =0,
=
,=
, 
(6) 
Form above , we can obtain voltage and current in which region as follows：
Region 1：
Region 2：
Region 3：