Polarization of Electric Field
Editors: 吳彬世
Advisor : Professor Jean-Fu
Kiang
By definition, the polarization is the characteristic that the locus of the tip of the electric field vector in time at a point in space. Here we discuss about electric field in EM-wave. To simplify the discussion, we decompose the electric field into two direction, $ \hat{x} $ and $ \hat{y} $, as two components, and let it propagate in the $ \hat{z} $ direction. For a uniform plane wave propagating in an arbitrary direction, that is: $$ \bar{E} = \bar{E_0}e^{-j\bar{k}\cdot\bar{r}}$$ where $\bar{k}$ is the direction of propagation, and the $\bar{r}$ is the position vector, such as $ \hat{x}x + \hat{y}y + \hat{z}z$ in Cartesian coordinate.
We consider that if the wave propagating in $+\hat{z}$ direction, then $\bar{E} = \bar{E_0}e^{-j\bar{k}\cdot\bar{r}}$ with $\bar{k} = \hat{z}k$. Here we use the phasor notation $E_x$ and $E_y$ to be two decomposition in the $\hat{x}$ and $\hat{y}$ direction. Due to $\bar{k} = \hat{z}k$, the total electric field after the calculation of dot product can be represented as: $$ \bar{E}(\bar{r}) = \hat{x}E_{x}e^{-jkz} + \hat{y}E_{y}e^{-jkz} $$
Because we want to discuss the polarization of the electric field, we need to find the relation between the part of $\hat{x}$ direction and $\hat{y}$ direction. Let $E_x$ and $E_y$ have a phase difference of $\phi$, and the amplitude ratio of $\hat{y}$ direction to the $\hat{x}$ direction is A. That is $\frac{E_y}{E_x} = Ae^{j\phi}$. Thus, we have: $$ \bar{E}(\bar{r}) = \hat{x}E_{x}e^{-jkz} + \hat{y}AE_{x}e^{j\phi}e^{-jkz} $$
Analyze the polarization at a fixed point, that is, fixed z=0. We will demonstrate several situation in A (amplitude) and $\phi$ (phase angle). Note that $\bar{E} = Re\{\bar{E}\}$ and amplitude of $E_x$ is $E_0$. We demonstrate the electric field's oscillating direction and amplitude as a vector. By observating the characteristic of the electric field on z=0 (xy-plane), we can easily know the type of polarization.
Case (1): $\phi = 0$ ( Linear Polarization )
$ \bar{E}(0, t) = \hat{x}E_{0}\cos(\omega t) + \hat{y}AE_{0}\cos(\omega t) $
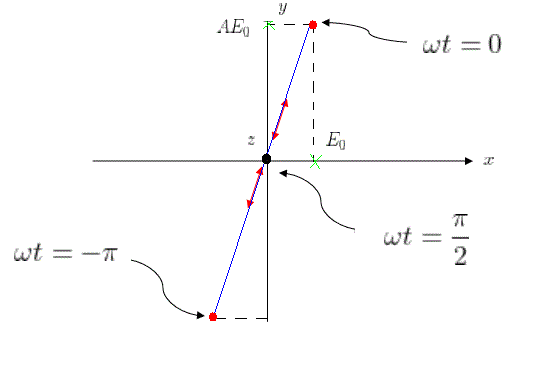
Since the electric field oscillates along a line, it is called linear polarization.
Case (2): $\phi = \frac{\pi}{2}, A = 1$ ( Circular Polarization )
$ \bar{E}(0, t) = \hat{x}E_{0}\cos(\omega t) - \hat{y}E_{0}\cos(\omega t) $
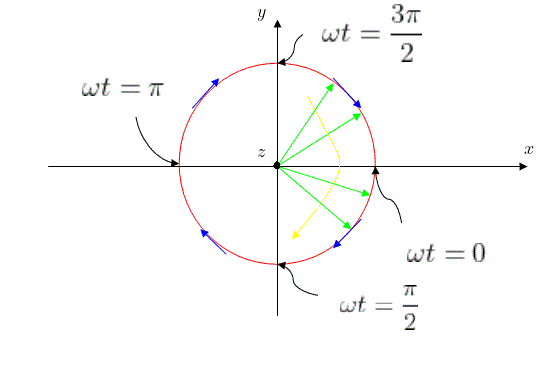
The electric field's oscillating direction and amplitude vector will rotate on a circle, hence it is called circular polarization.
Case (3): $\phi = \frac{\pi}{2}, A \ne 1$ ( Elliptical Polarization )
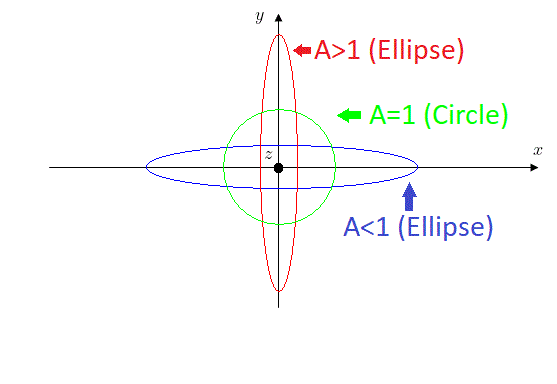
The electric field's oscillating direction and amplitude vector will rotate on an ellipse, hence it is called elliptical polarization.
l
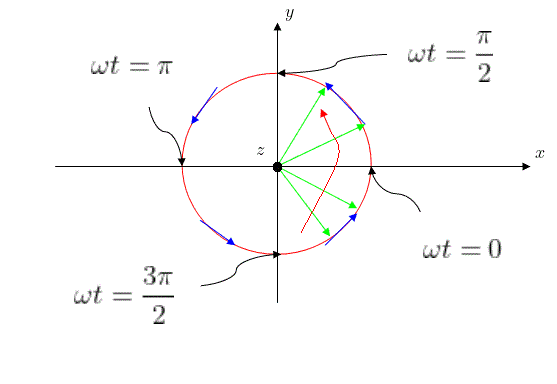
Left-hand and Right-hand Polarization ( LH. and RH. ):
If the vector rotates in the clockwise sense, we call it right-hand polarization, i.e. as t increases, the phasor angel of electric field will decrease. On the other hand, it will rotate in the counterclockwise sense and is called left-hand polarization.
For example , case (2) is left-hand polarization. If $\phi = -\frac{\pi}{2}$, we have a right-hand polarization: $ \bar{E}(0, t) = \hat{x}E_{0}\cos(\omega t) + \hat{y}AE_{0}\sin(\omega t) $
The simulations below show the oscillating direction and amplitude vector in 3D view, on xy-plane, and looking from +z-axis.
(1) Linear polarization
Aerial view and x-y cross-sectional view
(2) Right-hand circular polarization ( RHCP )
Aerial view and x-y cross-sectional view
Perspective view on z - axis
(3) Left-hand
elliptical polarization ( LHEP ) : A = 0.5
Perspective view on z- axis
(4) Left-hand
elliptical polarization ( LHEP ) : A = 2
Aerial view and x-y cross-sectional view
Perspective view on z- axis