Wave In Media
Consider waves in different media.
By using Ohm's Law: \( \bar{J} = \sigma \bar{E} \)
The Ampere's law can be expressed as:
\( \nabla\times\bar{H} = j\omega\varepsilon_0\bar{E}+\sigma\bar{E} \)
Define \( \underline{\varepsilon} = \varepsilon_0+\displaystyle\frac{\sigma}{j\omega}\underline{\varepsilon} \), the Ampere's law can be reduced to \( \nabla\times\bar{H} = j\omega\underline{\varepsilon}\bar{E} \)
The Faraday's law is \( \nabla\times\bar{E} = -j\omega\mu_0\bar{H} \)
Consider a plane wave solution \( \bar{E}(\bar{r}) = \hat{x}E_0e^{-j\bar{k}z} \), where \( \underline{k} = \omega\sqrt{\mu_0(\varepsilon_0+\displaystyle\frac{\sigma}{j\omega})} \)
(1) If the medium is copper, \( \displaystyle\frac{\sigma}{j\omega} \gg \varepsilon_0 \), and the wave number can be approximated as
$$ \underline{k} = \sqrt{j\omega\mu_0\sigma} = (1-j)\sqrt{\frac{\omega\mu_0\sigma}{2}} = \frac{1-j}{\delta}, \delta = \sqrt{\frac{2}{\omega\mu_0\sigma}} $$The time variation of electric field becomes
$$ \text{Re}\left\{e^{-j\underline{k}z}\cdot e^{j\omega t}\right\} = \text{Re}\left\{e^{-(1+j)z/\delta}\cdot e^{j\omega t}\right\} = e^{-\frac{z}{\delta}} \cos \left(\omega t - \frac{z}{\delta}\right) $$If \( \mu_0 = 4\pi\times 10^7, \varepsilon_0 = \displaystyle\frac{1}{36\pi}\times 10^{-9}, \omega = 2\pi\times 10^9 \ \rm{rad/s}, \sigma = 10^{-6} \).
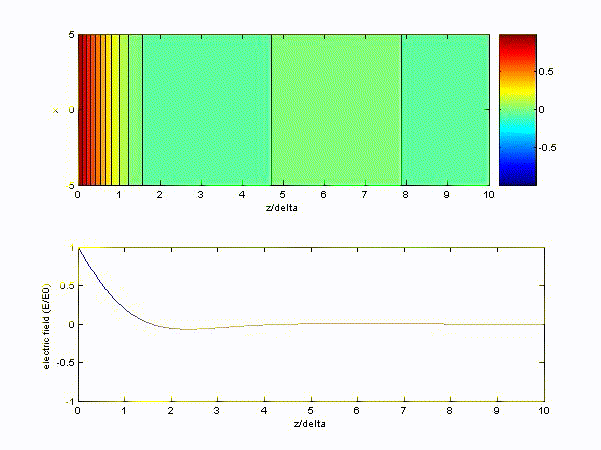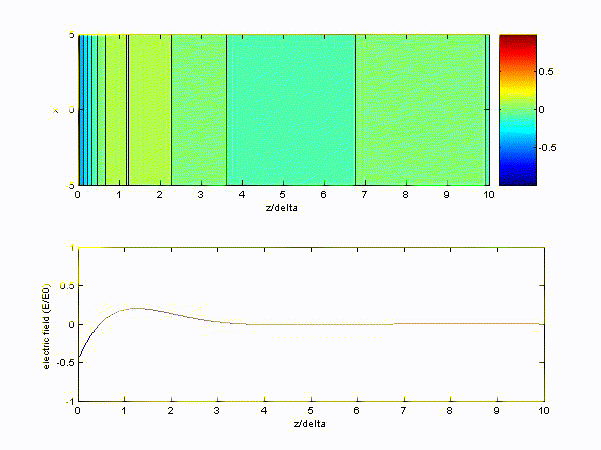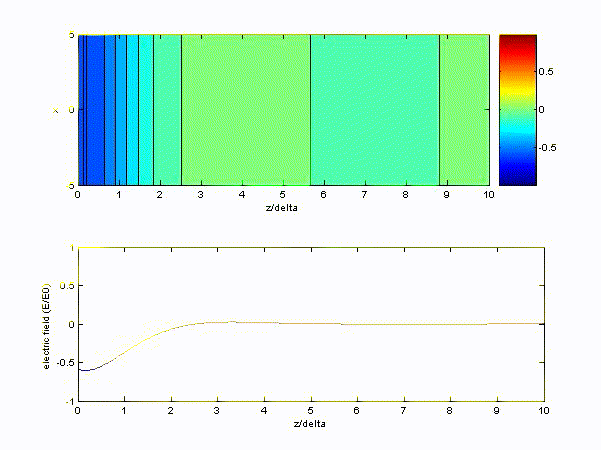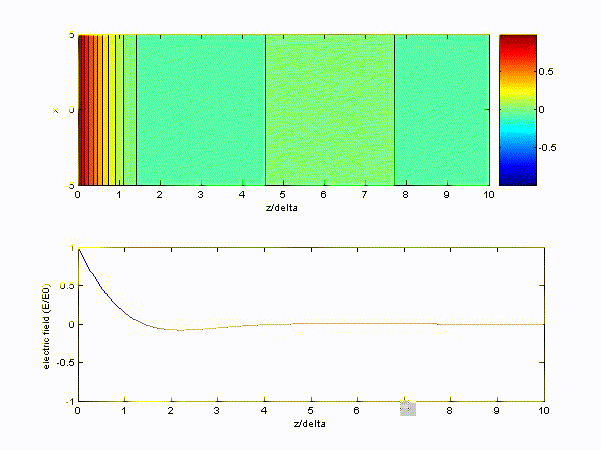
(2) If the medium is ice, the wave number can be approximated as
$$ \underline{k} = \omega\sqrt{\mu_0\varepsilon_0} \cdot \sqrt{1-j\frac{\sigma}{\omega\varepsilon_0}} \approx \omega\sqrt{\mu_0\varepsilon_0}\left(1-j\frac{\sigma}{\omega\varepsilon_0}\right) = k' - jk'' $$
where \( k' = \omega\sqrt{\mu_0\varepsilon_0} \) and \( k'' = \displaystyle\frac{\sigma\sqrt{\mu_0\varepsilon_0}}{2\varepsilon_0} \).
The time variation of electric field becomes
$$
\text{Re}\left\{e^{-j\underline{k}z}\cdot e^{j\omega t}\right\} = \text{Re}\left\{e^{-jk'z-k''z}\right\} = e^{-k''z}\cos(\omega t - k'z)
$$
If \( \mu_0 = 4\pi\times 10^7, \varepsilon_0 = \displaystyle\frac{1}{36\pi}\times 10^{-9}, \omega = 2\pi\times 10^9 \rm{rad/s}, \sigma = 10^{-6} \).
thus \( k' = 20.944 \) and we let it be \( k_1 \),
\( k'' = 0.0001885 \) and we let it be \( k_2 \).
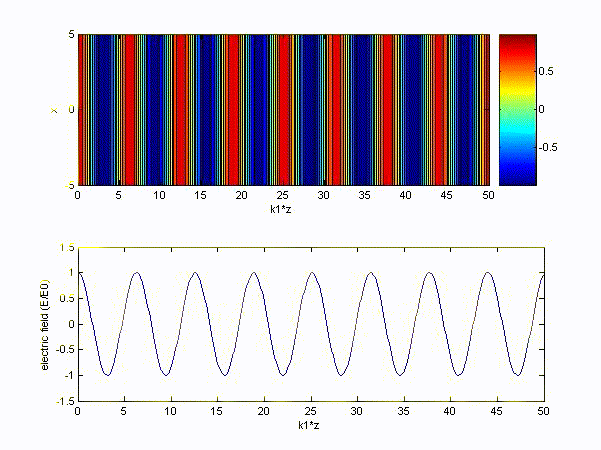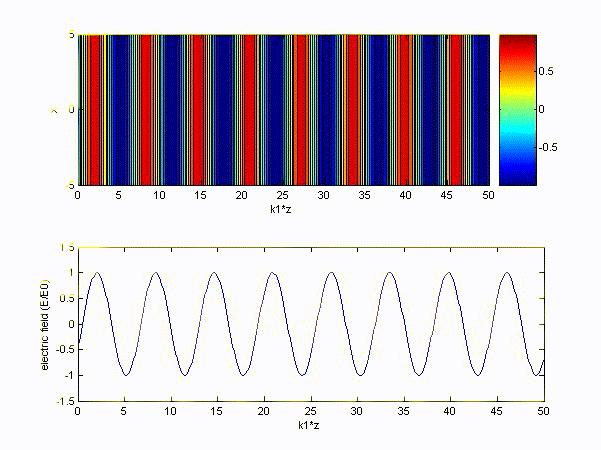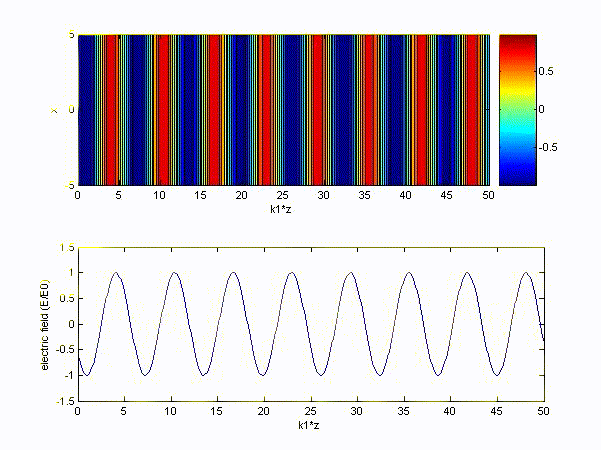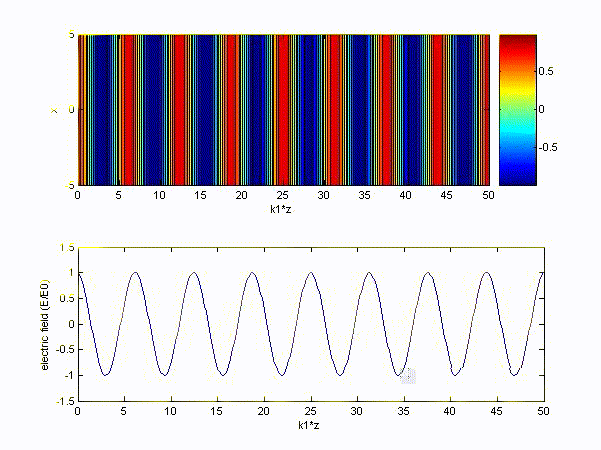
(3) In the ionosphere, charges follow the Newton's law: \( m\displaystyle\frac{\partial \bar{\nu}}{\partial t} = q\bar{E} \)
Let \( \bar{\nu}(\bar{r}, t) = \text{Re}\left\{\nu(\bar{r})\cdot e^{j\omega t}\right\} \)
then the equation of motion becomes \( j\omega m\nu = q\bar{E} \).
Since \( \bar{J} = nq\bar{\nu} \), the Ampere's law can be expressed as
where \( \omega_p^2 = \displaystyle\frac{nq^2}{m\varepsilon_0} \) is the plasma frequency.
Consider a plane wave solution \( \bar{E} = \hat{x}E_0 e^{-j\underline{k}z} \)
We have
\(
\begin{equation}
\underline{k} = \omega\sqrt{\mu_0\varepsilon_0(1-\omega_p^2 / \omega^2)} =
\left\{
\begin{array}{lr}
\beta, &\omega > \omega_p \\
-j\alpha, &\omega < \omega_p
\end{array}
\right.
\end{equation}
\)
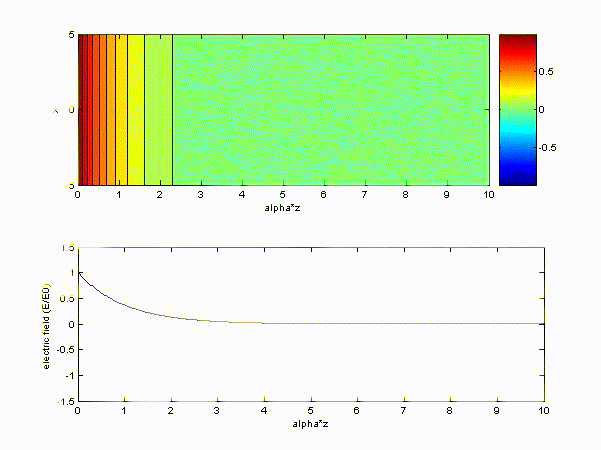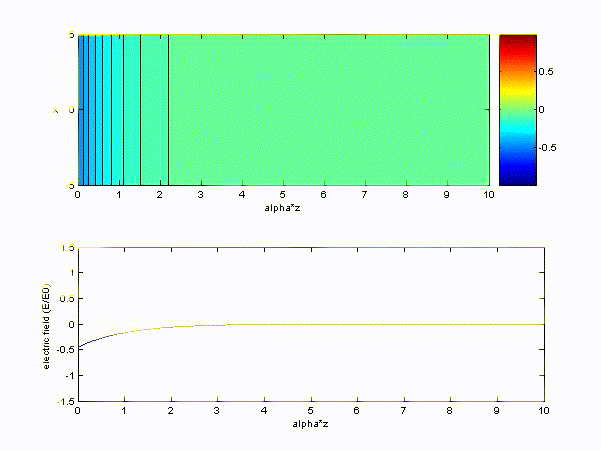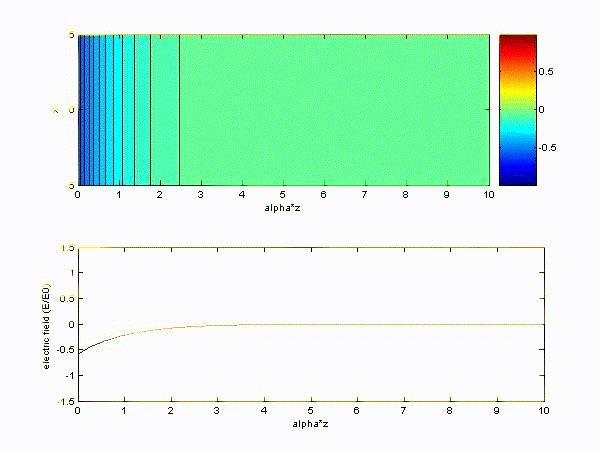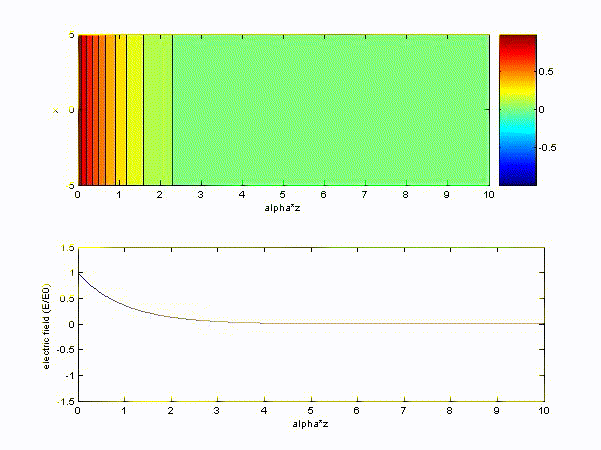
The time variation of electric field becomes
If \( q = 1.6\times 10^{-19}, m = 9.1\times 10^{-31}, n = 10^{18}, \varepsilon_0 = \displaystyle\frac{1}{36\pi}\times 10^{10} \rm{rad/s} \),
we find plasma frequency \( \omega_p = 1.7955\times 10^{10} \rm{rad/s} \)
(a) \( \omega > \omega_p\ (choose\ \omega = 10\omega_p) \) and choose x-axis to be '\(z/\beta\)'
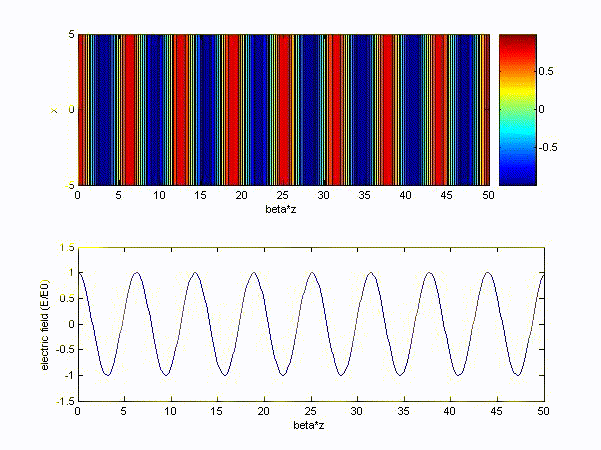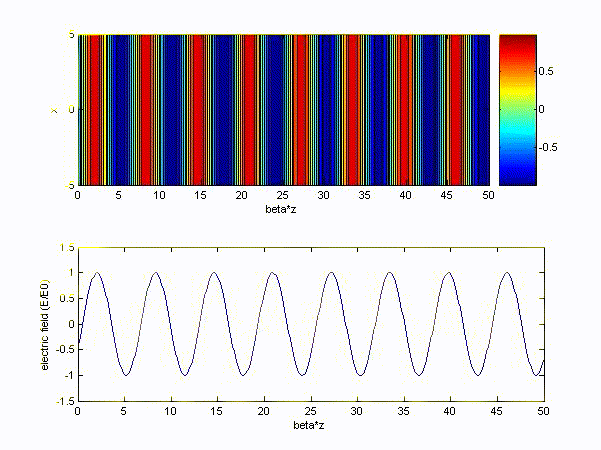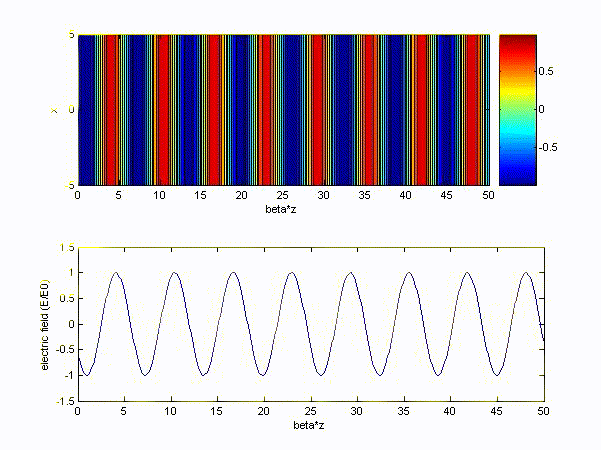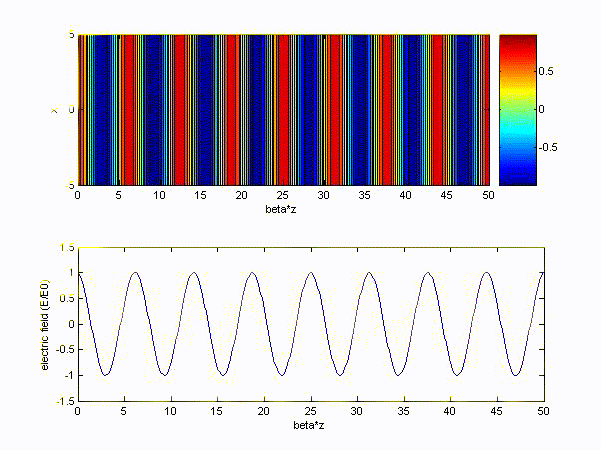
(b) \( \omega < \omega_p\ (choose\ \omega = 0.1\omega_p) \) and choose x-axis to be '\(z/\alpha\)'