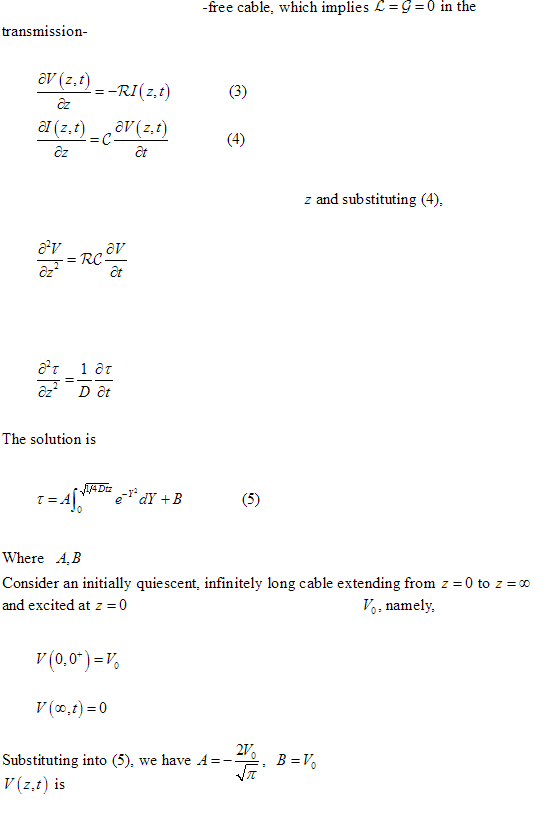Editors: ?¦óº³©ú¡B§õ©s«Û Advisor: ¦¿Â²´I ƒvƒwƒvƒwƒvƒwƒvƒw,,,,IztVzztVztzIztzt„gƒyƒ´ƒ{ƒ­ƒ{ƒ´ƒ{ƒ´„gƒÂƒ¼ ƒvƒwƒvƒwƒvƒwƒvƒw,,,,VztIzztIztzVztzt„gƒyƒ´ƒ{ƒ­ƒ{ƒ´ƒ{ƒ´„gƒ·ƒ³ Divide both equations by zƒ´, and let 0zƒ´„_ to have ƒvƒwƒvƒwƒvƒw,,,VztIztIztzt„g„gƒ­ƒ{ƒ{„g„gƒÂƒ¼ (1) ƒvƒwƒvƒwƒvƒw,,,IztVztVztzt„g„gƒ­ƒ{ƒ{„g„gƒ·ƒ³ (2) Which are the transmission-line equations in time-domain.
Diffusion over Transmission Line
Consider the distributed equivalent circuit for a lossy transmission line.
Apply KCL and KVL to have
-free cable, which implies 0ƒ­ƒ­ƒ¼ƒ· in the transmission- ƒvƒwƒvƒw,,VztIztz„gƒ­ƒ{„gƒÂ (3) ƒvƒwƒvƒw,,IztVztzt„g„gƒ­„g„gƒ³ (4) z and substituting (4), 22VVzt„g„gƒ­„g„gƒÂƒ³ 221zDtƒäƒä„g„gƒ­„g„g The solution is 2140DtzYAedYBƒäƒ{ƒ­ƒy„Å (5) Where ,AB Consider an initially quiescent, infinitely long cable extending from 0zƒ­ to zƒ­„V and excited at 0zƒ­0V, namely, ƒvƒw00,0VVƒyƒ­ ƒvƒw,0Vt„Vƒ­ Substituting into (5), we have 02VAƒàƒ­ƒ{, 0BVƒ­ƒvƒw,Vzt is
Consider a noninductive, leakage
line equations. Equations (1) and (2) reduce to
Taking the partial derivative of (3) with respect to
Which has the form of diffusion equation
are constants to be determined from boundary conditions.
by a constant voltage source of value
. Hence, the particular solution of
ƒvƒw2244000000022,1erfc4tztzYYVVztedYVVedYVztƒàƒàƒ{ƒ{„¹„É„¹„Ƀ­ƒ{ƒyƒ­ƒ{ƒ­„º„Ê„º„Ê„º„Ê„»„Ë„»„˄ńу³ƒÂƒ³ƒÂƒ³