Pulse Broadening in Dispersive Medium
Hung-yi Lo, Yu-tsung Lo, Yi-yun Chiu, and Che-jung Chuang
Advisor: Prof. Jean-Fu Kiang
From the dispersion curve, we know that the group velocity at higher frequency is greater than that at lower frequency. Consider a pulse in time domain having a certain bandwidth in frequency domain. Over a given distance, the lower frequencies undergo longer group delays than the higher frequencies, hence broadening the pulse in the time domain.
Consider the propagation of an amplitude-modulated signal consisting of a carrier frequency \(\omega_0\) modulated by a pulse having Gaussian envelope in time domain. Express the field at the input \((z=0)\) of the dispersive channel as \[E(0,t)=(E_0\cos\omega_0t)e^{-(t/T_0)^2}=E_0e^{-(t/T_0)^2}\cos\omega_0t\tag{1}\] Its associated complex form is \[E(0,t)=E_0e^{-(t/T_0)^2}e^{j\omega_0t}\tag{2}\] Note that \(e^{-(t/T_0)^2}\) presents the Gaussian envelope with its half-duration \(T_0\) which is when pulse amplitude decreases to \(1/e\) of its peak value. Our goal is to present \(E(z, t)\) with respect to \(E(0, t)\) to demonstrate the pulse broadening phenomenon. First, take the Fourier transform of \((2)\) to have \begin{align} E(0,\omega) & = \int\limits_{-\infty}^{\infty}E(0,t)e^{-j{\omega}t}\mathrm{d}t\\ & = E_0\int\limits_{-\infty}^{\infty}e^{-(t/T_0)^2}e^{-j(\omega-\omega_0)t}\mathrm{d}t\\ & = 2E_0\int\limits_0^{\infty}e^{-(t/T_0)^2}\cos(\omega-\omega_0)t\mathrm{d}t\\ & = \sqrt{\pi}E_0T_0e^{-(1/4)(\omega-\omega_0)^2T_0^2}\tag{3} \end{align} Each frequency component of the signal travels in the dispersive medium with different phase change \(e^{-j\beta_zz}\) at \(z\). Thus, the signal at \(z\) can be expressed as \[E(z,{\omega})=E(0,{\omega})e^{-j\beta_zz}\tag{4}\] Taking the inverse Fourier transform of \((4)\), we obtain the propagated signal as \[E(z,t)=\frac{1}{2\pi}\int\limits_{-\infty}^{\infty}E(z,{\omega})e^{j{\omega}t}\mathrm{d}\omega=\frac{1}{2\pi}\int\limits_{-\infty}^{\infty}E(0,{\omega})e^{-j\beta_zz}e^{j{\omega}t}\mathrm{d}\omega\tag{5}\]
Considering a narrow-band signal centered at \(\omega_0\), expand \(\beta_z\) in Taylor's series about \(\omega_0\) and keep the first three terms to have \[\beta_z(\omega)=\beta_z^{(0)}+(\omega-\omega_0)\beta_z^{(1)}+\frac{1}{2}(\omega-\omega_0)^2\beta_z^{(2)}\tag{6}\] Where \(\beta_z^{(0)}\), \(\beta_z^{(1)}\), and \(\beta_z^{(2)}\) are \(\beta_z\), \(\mathrm{d}\beta_z/\mathrm{d}\omega\), \(\mathrm{d}\beta_z^2/\mathrm{d}\omega^2\) evaluated at \(\omega=\omega_0\). Substituting \((6)\) in \((5)\), we obtain \begin{align} E(z,t) & = \frac{1}{2\pi}\int\limits_{-\infty}^{\infty}E(0,\omega)e^{-j\beta_z^{(0)}z-j(\omega-\omega_0)\beta_z^{(1)}z-j(\frac{1}{2})(\omega-\omega_0)^2\beta_z^{(2)}z}e^{j{\omega}t}\mathrm{d}\omega\\ & = \frac{1}{2\pi}\int\limits_{-\infty}^{\infty}E(0,\omega')e^{-j\beta_z^{(0)}z-j\omega'(t-t_0)-j(\frac{1}{2})(\omega')^2\beta_z^{(2)}z}e^{j\omega_0t}\mathrm{d}\omega'\tag{7} \end{align} where \(\omega'=\omega-\omega_0\) and we defined group delay \(t_0\) as \[t_0=z\beta_z^{(1)}=\frac{z}{\left.v_g\right|_{\omega_0}}\tag{8}\] For a narrow-band signal, the group velocity can be approximated as \(v_g=\mathrm{d}\omega/\mathrm{d}\beta_z\) calculated at the center frequency. Thus, we obtain \[E(z,t)=\frac{E_0}{\sqrt{1+j(S/T_0)}}e^{\frac{-(t-t_0)^2}{T_0^2+S^2}}e^{j\left\{\frac{(t-t_0)^2S}{T_0(T_0^2+S^2)}+\omega_0t-\beta_z^{(0)}z\right\}}\tag{9}\] Define pulse broadening parameter \(S\) as \[S=\frac{2}{T_0}\beta_z^{(2)}z=\frac{2}{T_0}\frac{{\partial}t_0}{\partial\omega_0}\tag{10}\] Note that \(E(0,t)\) in \((2)\) is obtained by setting \(z=0\) in \((9)\). The input signal at \(z=0\), reaches its maximum at \(t=0\); at distance \(z\), \(E(z,t)\) reaches its maximum at \(t=t_0\), which is the time the frequency component at \(\omega_0\) reaches \(z\). The half duration is equal to \(\sqrt{T_0^2+S^2}\) as derived from \((9)\). In comparison, the half duration of \(E(0,t)\) is \(T_0\) from \((2)\). The signal(pulse) actually experiences broadening in a dispersive medium.
In this simulation, the wave is transmitting in fiber optics, which is assumed to have a refraction index of \(1.333\). We also assume that the initial amplitude of the wave \(E_0\) is \(5\mathrm{(V/m)}\), the carrier freuquency \(\omega_0\) is \(2\pi{\times}3{\times}10^{14}\mathrm{(rad/s)}\), and the half-duration of the Gaussian envelope \(T_0\) is \(3{\times}10^{-15}\mathrm{(s)}\).
Substituting the above constants in (2), we obtain
\[E(0,t)=5e^{\left\{ j 6 \pi \times 10^{14} t – \frac{1}{9} \times 10^{30} t^2 \right\}}\]
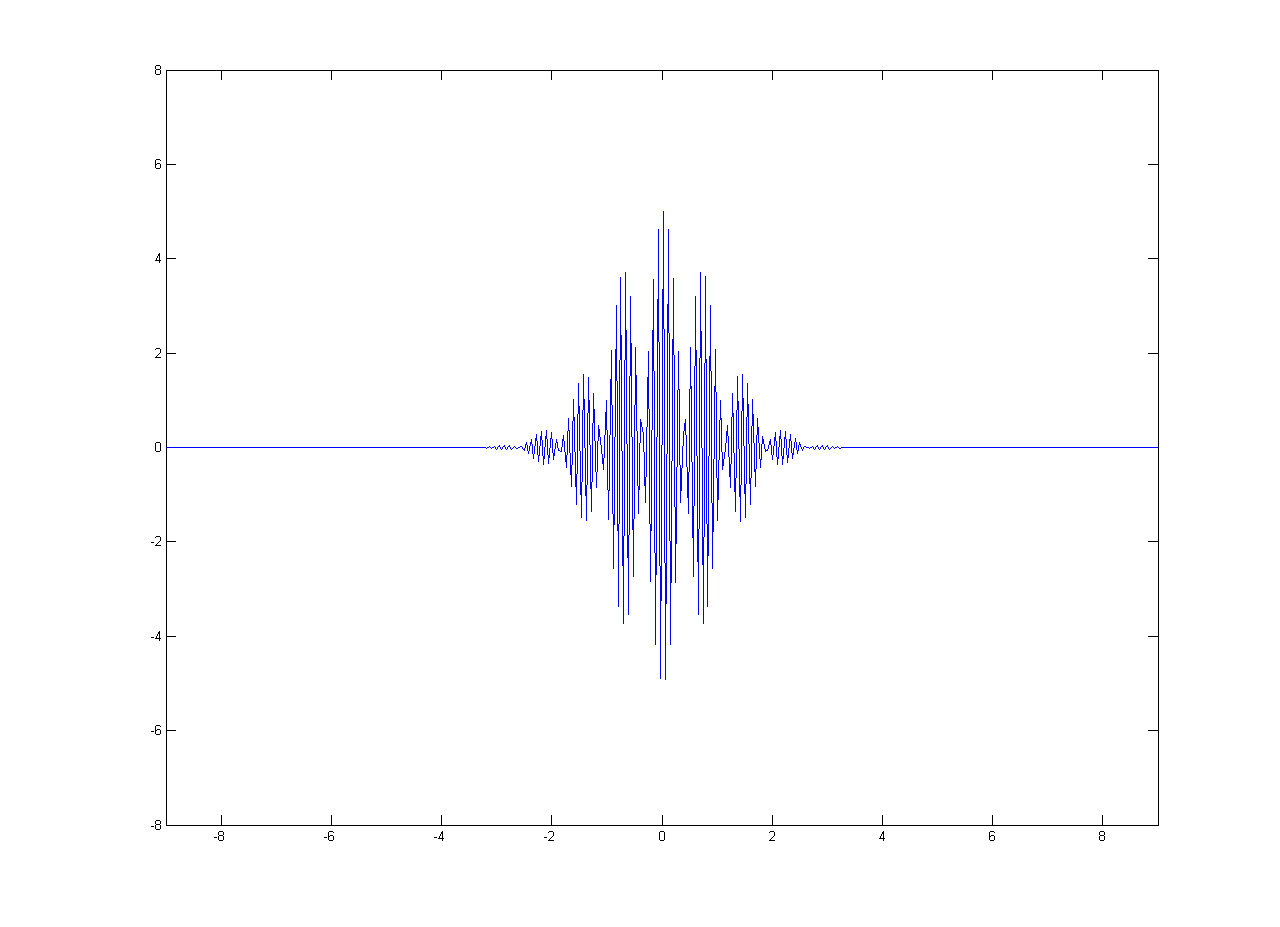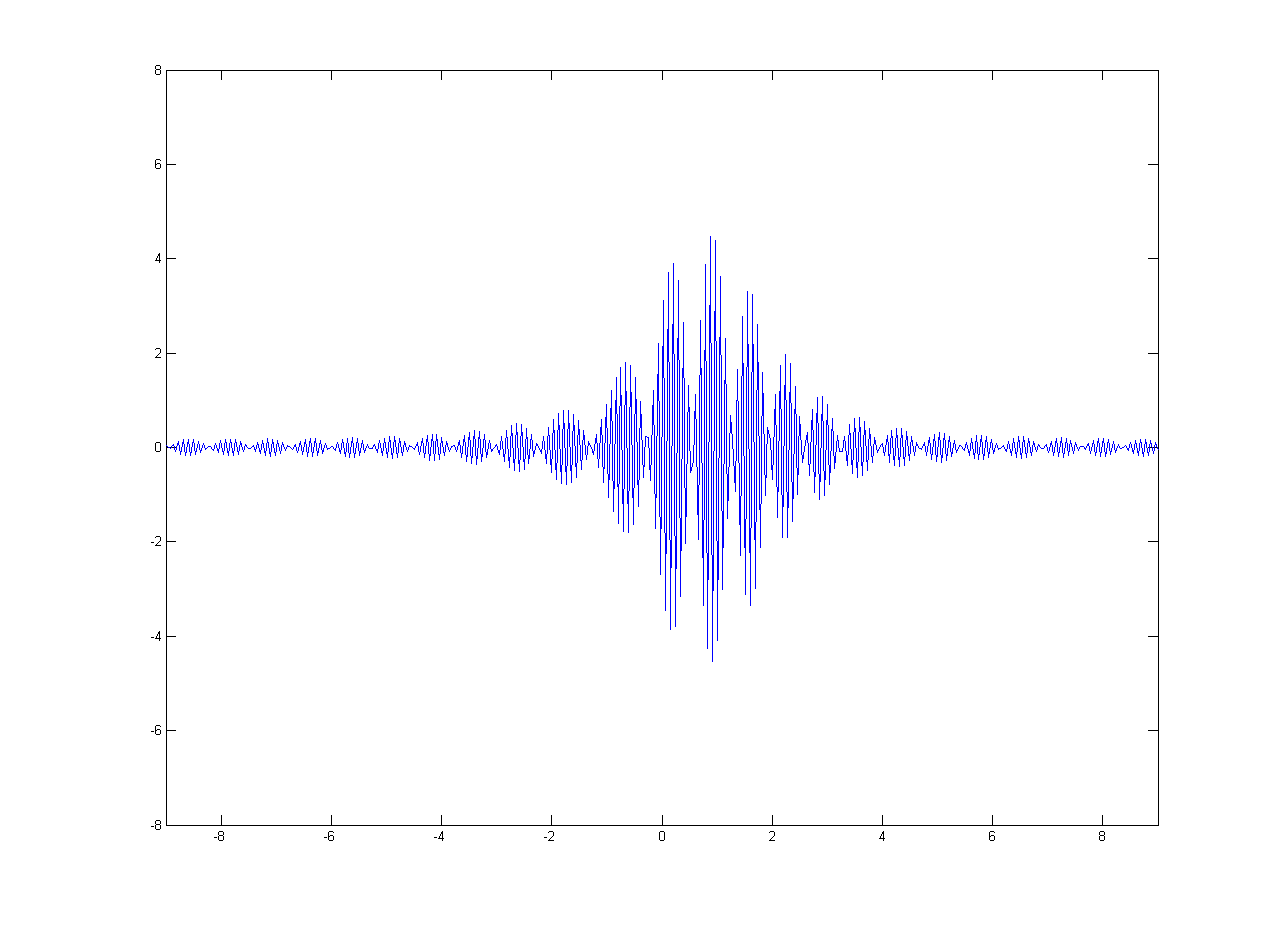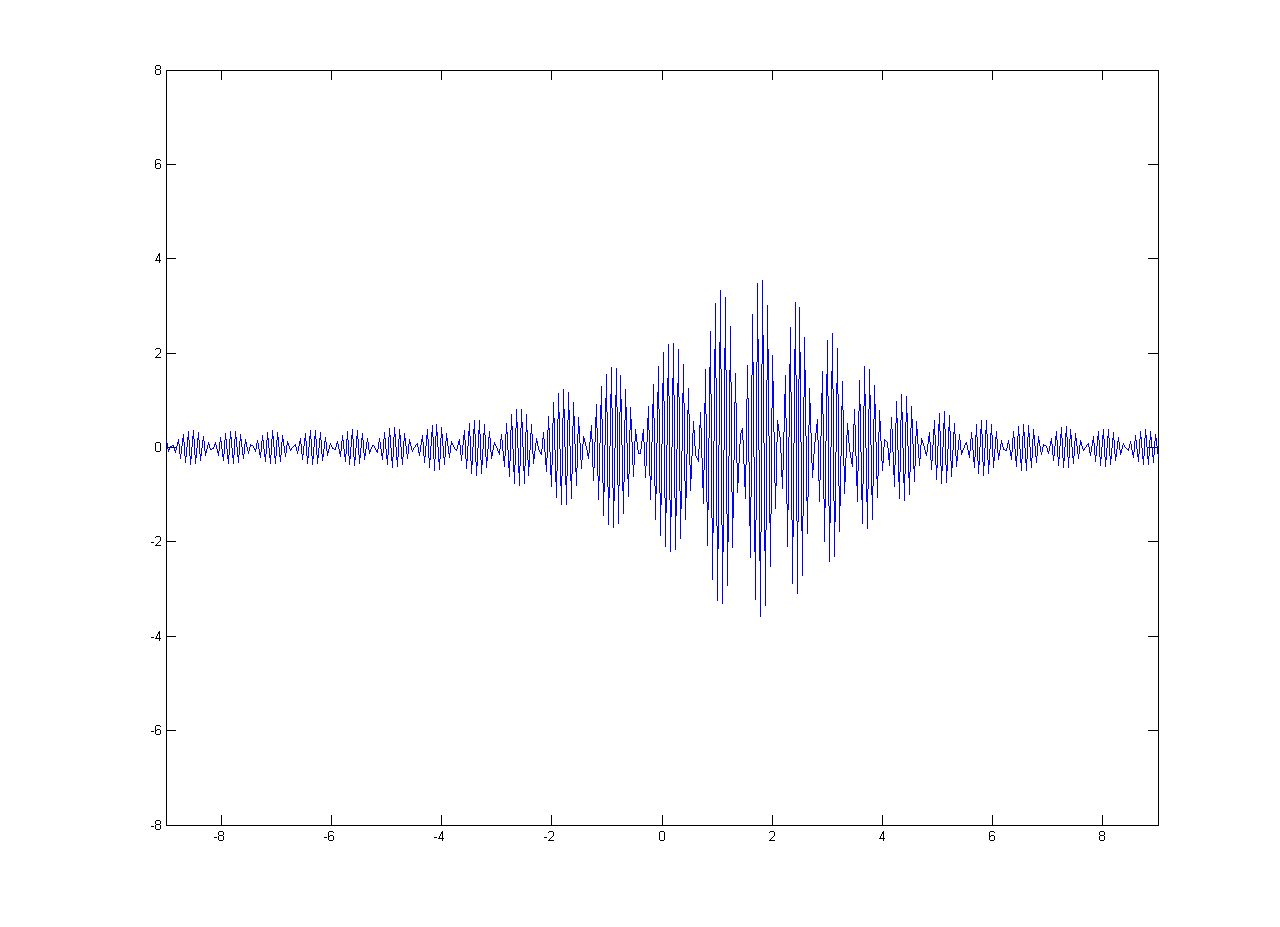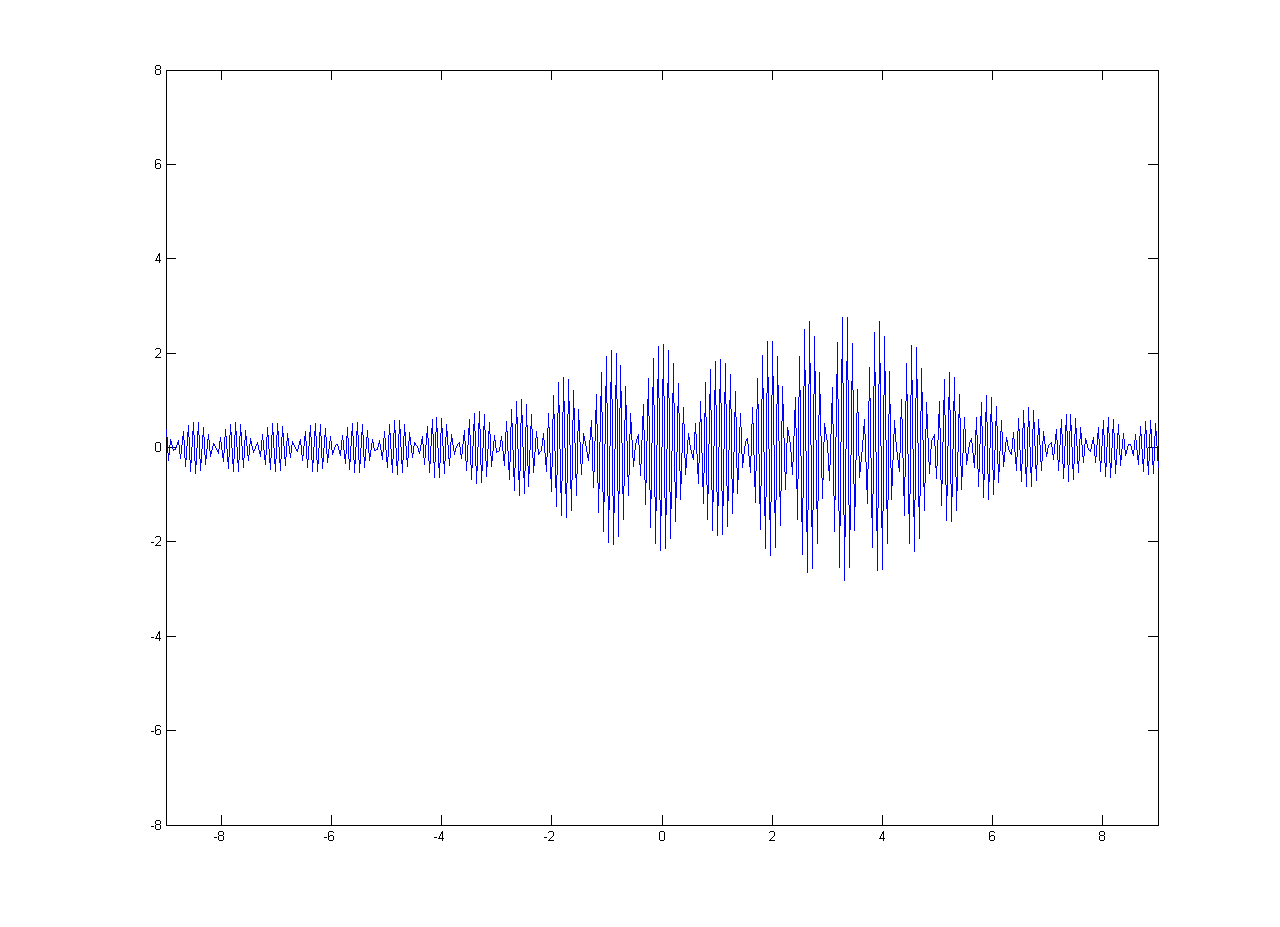 Amplitude \(\mathrm{(V/m)}\)
\(z-z_0 (\mu\mathrm{m})\)
Amplitude \(\mathrm{(V/m)}\)
\(z-z_0 (\mu\mathrm{m})\)