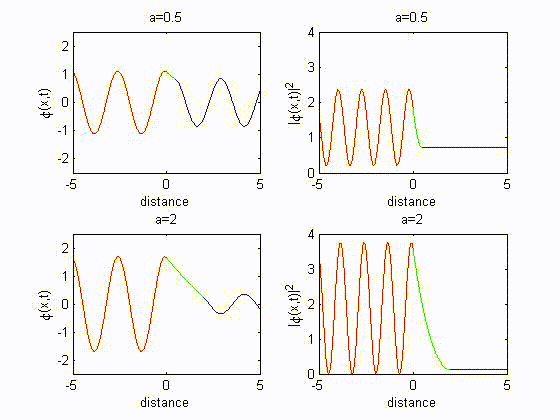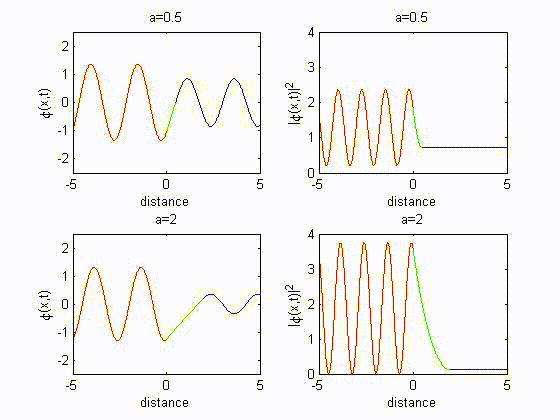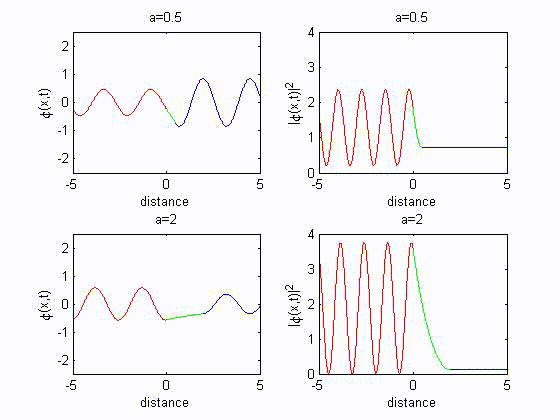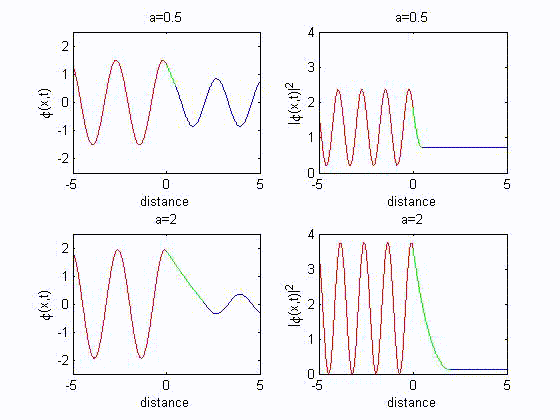
B. Behavior of $\varphi(x)$ at a potential discontinuity
Consider a potential $V_{\varepsilon}(x)$ which equal to $V(x)$ outside the interval
$[x_1-\varepsilon, x_1+\varepsilon]$ , and varying continuously within this interval. Consider the
Schrödinger equation:
$\dfrac{d^2}{dx^2}\varphi_{\epsilon}(x)+\dfrac{2m}{\hbar^2}[E-V_{\varepsilon}(x)]\varphi_{\varepsilon}(x)=0\qquad\qquad\qquad\qquad\qquad\qquad\enspace (6)$
where $V_{\varepsilon}(x)$ is assumed to be bounded, independently of $\varepsilon$, within the
interval $[x_1-\varepsilon, x_1+\varepsilon]$. Choose a solution $\varphi_{\varepsilon}(x)$, in $x\lt x_1-\varepsilon$, which
coincides with a given solution to (1). Assume that $\varphi_{\varepsilon}(x)$ remains
bounded in the neighborhood of $x=x_1$. Physically, this means that the
probability density remains finite. Then, integrating (6) between
$x_1-\delta$ and $x_1+\delta$, we obtain:
$\begin{align} \dfrac{d\varphi_{\varepsilon}}{dx}(x_1+\delta)-\dfrac{d\varphi_{x}}{dx}(x_1-\delta)=\dfrac{2m}{\hbar^2}\int_{x_1-\delta}^{x_1+\delta}{[V_{\epsilon}(x)-E]\varphi_{\epsilon}(x)dx}\qquad (7) \end{align}$
At the limit $\varepsilon\to0$, the function to be integrated on the right-hand
side of this expression remains bounded. Consequently, if $\delta$ approaches
zero, the integral also approches zero. Then, we have
$\dfrac{d\varphi}{dx}(x_1+\delta)-\dfrac{d\varphi}{dx}(x_1-\delta)\to 0\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\enspace (8)$
which implies $\dfrac{d\varphi}{dx}$ is continuous at $x=x_1$
Next, consider two special cases.
Case 1: tunneling effect
The solution in three regions I($x<0$), II($0<x<a$) and III($x>a$) are
$\varphi_{1}(x)=Ae^{ik_1x}+Be^{-ik_1x}$
$\varphi_{2}(x)=Ce^{-\rho_2x}+De^{\rho_2x}$
$\varphi_{3}(x)=Fe^{ik_1x}+Ge^{-ik_1x}$
Since there is no reflection in region III, $G$ is set to zero.
Without loss of generality, set $A=1.$
Impose the boundary condition to have
$1+B=C+D$ $\qquad\qquad\qquad\qquad\qquad(\varphi(x)$ is continuous at $x=0)$
$ik_1-ik_1B=\rho_2D-\rho_2C$ $\qquad\qquad\qquad(\dfrac{d\varphi}{dx}$ is continuous at $x=0)$
$Ce^{-\rho_2a}+De^{\rho_2 a}=Fe^{ik_1a}$ $\qquad\qquad\qquad\quad(\varphi(x)$ is continuous at $x=a)$
$-\rho_2Ce^{-\rho_2a}+\rho_2De^{\rho_2a}=ik_1Fe^{ik_1a}$ $\qquad\quad(\dfrac{d\varphi}{dx}$ is continuous at $x=a)$
Thus, we have
$C=\dfrac{2ik_1e^{2\rho_2a(\rho_2-ik_1)}}{(\rho_2+ik_1)^2-(\rho_2-ik_1)^2e^{2\rho_2a}}$
$D=\dfrac{2ik_1(\rho_2+ik_1)}{(\rho_2+ik_1)^2-(\rho_2-ik_1)^2e^{2\rho_2a}}$
$B=\dfrac{(\rho_2^2+k_1^2)(e^{2\rho_2a-1})}{(\rho_2+ik_1)^2-(\rho_2-ik_1)^2e^{2\rho_2a}}$
$F=\dfrac{4ik_1\rho_2e^{(\rho_2-ik_1)a}}{(\rho_2+ik_1)^2-(\rho_2-ik_1)^2e^{2\rho_2a}}$
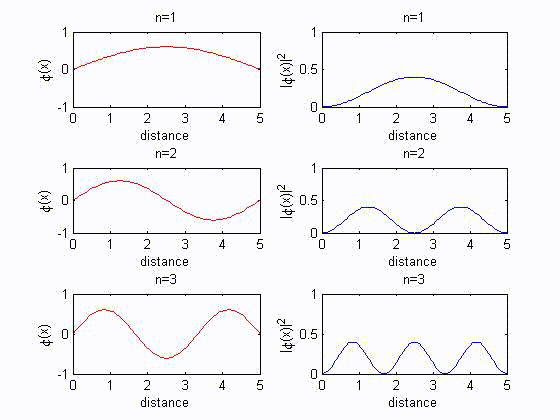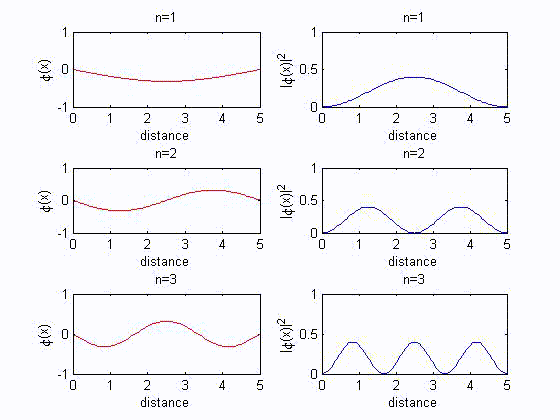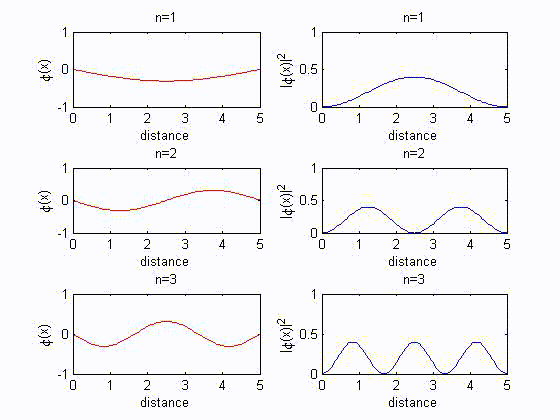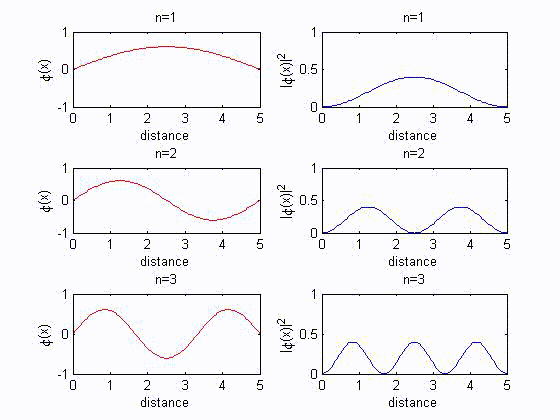
Case 2: particle in a box
The solution in the three region I($x<0$), II($0<x<a$), III($x>a$) are
$\varphi_1(x)=0$
$\varphi_2(x)=Ce^{-ik_2x}+De^{ik_2x}$
$\varphi_3(x)=0$
Impose the boundary condition to have
$C+D=0$
$Ce^{-ik_2a}+De^{ik_2a}=0$
Thus, we have
$C=-D$
$\sin{k_2a}=0$(It means $k_2a=n\pi$ for $n=1, 2, 3, ...$)
$\varphi_2(x)=2D\sin{\left(\dfrac{n\pi}{a}x\right)}$ or $\varphi_2(x)=A\sin{\left(\dfrac{n\pi}{a}x\right)}$
In order to find $A$, we recognize that the particle must exist somewhere in space, so the integral of $|\varphi(x)|^2$ over all $x$
, which corresponds to the probability of finding the particle somewhere, is equal to $1$:
$\begin{align}1=\int_{-\infty}^{\infty}{|\varphi(x)|^2dx}=|A|^2\int_{-\infty}^{\infty}{\sin^2{\left(\dfrac{n\pi}{a}x\right)}}=|A|^2\left(\dfrac{a}{2}\right)\end{align}$
or
$|A|=\sqrt{\dfrac{2}{a}}$