Partial-Cone Abstraction and Refinement Algorithm

Description

In this project, we would like to devise a ¡§Partial-Cone Abstraction and Refinement (PCAR)¡¨ algorithm in which a partial-cone SAT problem is first solved and then its corresponding assignment is used to guide the abstraction and refinement of the concrete (complete) SAT problem.

Let¡¦s first suppose the SAT target is an n-output combinational circuit as shown below, where { y₁, y₂¡K y_n } and { x₁, x₂¡K, x_m } are the output and input signals, respectively.

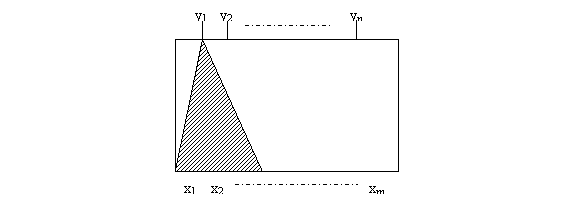
Our SAT target is to find an input assignment such that the outputs y₁ = 1, y₂ = 1,¡K and y_n = 1 are satisfied at the same time. However, suppose it is very hard to satisfy the above targets together. Therefore, we would like to develop the following PCAR algorithm:

(a) Pick one of the output, say ¡§y₁¡¨, and solve the partial target/cone ¡§y₁ = 1¡¨ first. If the partial target is NOT satisfiable, then the original problem is UNSAT too. Otherwise, let the assignment A₁ = { a₁, a₂,¡K, a_j } be one of the input vectors to satisfy the partial cone SAT problem.

(b) Include one or more outputs to the SAT target. Extend the partial assignment A₁ to this new problem. If the problem becomes UNSAT, then we can extract the UNSAT core which is sufficient to refute the partial assignment A₁. Or alternatively, we can identify a subset of the assignments A₁¡¦ in A₁ which are included in the UNSAT core. We can conclude that it is NOT possible to extend A₁¡¦ as a full assignment for the original problem.

(c) Go back to (a) to find another assignment that is disjunctive to A₁¡¦ in (b). Repeat until either a concrete solution is found, or the original problem can be proven UNSAT.

The above algorithm is still pre-mature. You should elaborate it and conduct experiments to make it a practical and useful SAT algorithm. You can also implement your algorithm on a CNF-based SAT solver.

Problem inputs

Ø Circuit-based SAT testcases (e.g. AIGER).

What you should do

1. Implement the above idea on an existing SAT solver, be it a CNF or circuit-based one.

2. Compare with the state-of-the-art SAT solvers.